题目内容
已知等差数列{an}的前n项和为Sn,满足Sn≥S5=-20,n∈N*,则数列公差d的取值范围是 .
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:由S5=-20得到首项和公差间的关系,代入Sn≥-20得到n(n-5)d≥8(n-5),分类讨论n后即可求得公差d的取值范围.
解答:
解:由S5=-20,得5a1+
=-20,
整理得:a1=-4-2d.
再由Sn=na1+
≥-20,得:
n(-4-2d)+
≥-20,
整理得:n(n-5)d≥8(n-5)①
当n=5时,对于任意实数d①式都成立;
当n≤4时,①式化为d≤
,
当n=4时,
取最小值2.
∴d≤2;
当n≥6时,①式化为d≥
,
当n=6时,
取最大值
.
∴d≥
.
综上,d的取值范围是
≤d≤2.
故答案为:
≤d≤2.
| 5×4d |
| 2 |
整理得:a1=-4-2d.
再由Sn=na1+
| n(n-1)d |
| 2 |
n(-4-2d)+
| n(n-1)d |
| 2 |
整理得:n(n-5)d≥8(n-5)①
当n=5时,对于任意实数d①式都成立;
当n≤4时,①式化为d≤
| 8 |
| n |
当n=4时,
| 8 |
| n |
∴d≤2;
当n≥6时,①式化为d≥
| 8 |
| n |
当n=6时,
| 8 |
| n |
| 4 |
| 3 |
∴d≥
| 4 |
| 3 |
综上,d的取值范围是
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题考查等差数列的前n项和,考查了数列的函数图象,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
相关题目
已知函数f(x)=
的定义域为[0,+∞),则实数a的取值范围为( )
| ||
| x3-3x+a |
| A、(0,3) |
| B、(0,2) |
| C、(2,+∞) |
| D、(3,+∞) |
已知函数f(x)=
-log2x,在下列区间中,包含f(x)零点的区间是( )
| 6 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,4) |
| D、(4,+∞) |
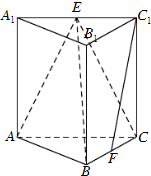 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.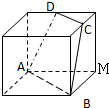 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是
如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是