题目内容
集合A={x|x2-2x<0},B={y|y=2x,x>0},R是实数集,则A∩B=( )
| A、(0,+∞) |
| B、(-∞,0)∪(2,+∞) |
| C、(0,1) |
| D、(1,2) |
考点:交集及其运算
专题:集合
分析:根据不等式的性质求出集合A,B,利用集合的基本运算即可得到结论.
解答:
解:∵A={x|x2-2x<0}={x|0<x<2},
B={y|y=2x,x>0}={x|x>1},
∴A∩B={x|1<x<2},
故选:D.
B={y|y=2x,x>0}={x|x>1},
∴A∩B={x|1<x<2},
故选:D.
点评:本题主要考查集合的基本运算,根据不等式的性质求出集合A,B是解决本题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知z1、z2∈C,|z1+z2|=2
,|z1|=
,|z2|=
,则|z1-z2|等于( )
| 2 |
| 3 |
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
若不等式|x+a|<6的解集为(-1,11),则实数a等于( )
| A、-1 | B、-7 | C、7 | D、-5 |
已知奇函数f(x)在x≥0时,f(x)=x2-4x,则使f(x-2)>-3成立的x的取值范围是( )
A、(-2-
| ||
B、(-4-
| ||
C、(-
| ||
D、(-∞,-
|
下列函数中,在(0,2)内有零点且单调递增的是( )
| A、y=2x-2 | ||
B、y=log
| ||
| C、y=|x|-3 | ||
| D、y=-x3 |
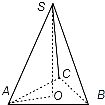 如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )
如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )