题目内容
若不等式|x+a|＜6的解集为（-1，11），则实数a等于（ ）
| A、-1 | B、-7 | C、7 | D、-5 |
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由不等式可得-6-a＜x＜6-a，再根据它的解集为（-1，11），可得-6-a=-1，6-a=11，由此解得a的值
解答：
解：由不等式|x+a|＜6，可得-6＜x+a＜6，即-6-a＜x＜6-a，
再根据它的解集为（-1，11），可得-6-a=-1，6-a=11，解得a=-5，
故选：D．
再根据它的解集为（-1，11），可得-6-a=-1，6-a=11，解得a=-5，
故选：D．
点评：本题主要考查绝对值不等式的解法，关键是去掉绝对值，属于基础题．
练习册系列答案
相关题目
方程x2+y2+ax-2ay+a2+3a=0表示的图形是半径为r（a＞0）的圆，则该圆 圆心在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若a＞b，则下列不等式正确的是（ ）
A、
| ||||
| B、a3＞b3 | ||||
| C、ac2＜bc2 | ||||
| D、a2＞b2 |
已知α∈（0，
），sinα=
，则cos（
-α）等于（ ）
| π |
| 2 |
| 4 |
| 5 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知a＞1，-1＜b＜0，那么（ ）
| A、ab＞b |
| B、ab＜-a |
| C、ab2＜ab |
| D、ab2＞b2 |
集合A={x|x2-2x＜0}，B={y|y=2x，x＞0}，R是实数集，则A∩B=（ ）
| A、（0，+∞） |
| B、（-∞，0）∪（2，+∞） |
| C、（0，1） |
| D、（1，2） |
若函数f（x）在R上可导，且满足f（x）＜xf′（x），则（ ）
| A、2f（1）＜f（2） |
| B、2f（1）＞f（2） |
| C、2f（1）=f（2） |
| D、f（1）=f（2） |
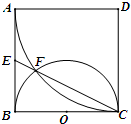如图，正方形ABCD边长为2，以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F，连结CF并延长交AB于点E．