题目内容
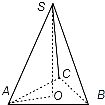如图，在三棱锥S-ABC中，底面是边长为1的等边三角形，侧棱长均为2，SO⊥底面ABC，O为垂足，则侧棱SA与底面ABC所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：直线与平面所成的角
专题：空间角
分析：SO⊥底面ABC，∠SAO即侧棱SA与底面ABC所成角，在Rt△SAO中计算即可得答案．
解答：
解：SO⊥底面ABC，O为垂足，∠SAO即侧棱SA与底面ABC所成角，
底面是边长为1的等边三角形，AO=
，
在Rt△SAO中，cos∠SAO=
=
=
故选D．
解：SO⊥底面ABC，O为垂足，∠SAO即侧棱SA与底面ABC所成角，底面是边长为1的等边三角形，AO=
| ||
| 3 |
在Rt△SAO中，cos∠SAO=
| AO |
| SA |
| ||||
| 2 |
| ||
| 6 |
故选D．
点评：本题考查线面角，先作后求的原则，属基础题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
已知点P（x，y）的坐标满足条件
，O为坐标原点，则直线OP的斜率取值范围是（ ）
|
| A、[3，5] |
| B、[2，5] |
| C、（-∞，3]∪[5，+∞） |
| D、（-∞，2]∪[5，+∞） |
若a＞b，则下列不等式正确的是（ ）
A、
| ||||
| B、a3＞b3 | ||||
| C、ac2＜bc2 | ||||
| D、a2＞b2 |
已知a＞1，-1＜b＜0，那么（ ）
| A、ab＞b |
| B、ab＜-a |
| C、ab2＜ab |
| D、ab2＞b2 |
集合A={x|x2-2x＜0}，B={y|y=2x，x＞0}，R是实数集，则A∩B=（ ）
| A、（0，+∞） |
| B、（-∞，0）∪（2，+∞） |
| C、（0，1） |
| D、（1，2） |
函数f（x）=2x+4x-3的零点所在区间是（ ）
A、（
| ||||
B、（-
| ||||
C、（0，
| ||||
D、（
|
若函数f（x）在R上可导，且满足f（x）＜xf′（x），则（ ）
| A、2f（1）＜f（2） |
| B、2f（1）＞f（2） |
| C、2f（1）=f（2） |
| D、f（1）=f（2） |
已知m，n是不同的两条直线，α，β是不同的两个平面，则下列命题中不正确的是（ ）
| A、若m∥n，m⊥α，则n⊥α |
| B、若m∥α，α∩β=n，则m∥n |
| C、若m⊥α，m?β，则α⊥β |
| D、若m⊥α，m⊥β，则α∥β |
