题目内容
在△ABC中，已知A=30°，b=2
，a=2，则角B等于（ ）
| 3 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
考点：正弦定理
专题：计算题,解三角形
分析：△ABC中，由正弦定理得
=
，即可求出B．
| 2 |
| sin30° |
2
| ||
| sinB |
解答：
解：△ABC中，∵A=30°，b=2
，a=2，
∴由正弦定理得
=
，
∴sinB=
，
∵b＞a，
∴B=60°或120°．
故选：D．
| 3 |
∴由正弦定理得
| 2 |
| sin30° |
2
| ||
| sinB |
∴sinB=
| ||
| 2 |
∵b＞a，
∴B=60°或120°．
故选：D．
点评：本题考查正弦定理的应用，考查学生的计算能力，属于基础题．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
对于x∈R，式子
恒有意义，则常数k的取值范围是（ ）
| 1 | ||
|
| A、0＜k＜4 |
| B、0≤k≤4 |
| C、0≤k＜4 |
| D、0＜k≤4 |
函数y=
的定义域为（ ）
| ||
| lnx |
| A、（0，1）∪（1，+∞） |
| B、（1，+∞） |
| C、（0，1） |
| D、（0，+∞） |
在四边形ABCD中，
=（2，4），
=（-6，3），则该四边形的面积为（ ）
| AC |
| BD |
A、3
| ||
B、2
| ||
| C、5 | ||
| D、15 |
设M、N是两个非空集合，且M={a|a∈N}，则M、N 间的关系为（ ）
| A、M=N | B、M是N的真子集 |
| C、M是N的子集 | D、M∈N |
复数（3m-2）+（m-1）i是虚数，则实数m应满足的条件是（ ）
| A、m≠1 | ||
B、m≠
| ||
| C、m=1 | ||
D、m=
|
若0＜b＜a＜1，则在ab，ba，aa，bb中最大值是（ ）
| A、ba |
| B、aa |
| C、ab |
| D、bb |
函数y=x2在区间[1，2]上的平均变化率为（ ）
| A、4 | B、5 | C、2 | D、3 |
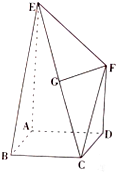如图，四边形ABCD是边长为2的正方形，AE⊥面ABCD，DF∥AE，AE=4，G为EC的中点，且GF∥面ABCD．