题目内容
9.定义:离心率e=$\frac{\sqrt{5}-1}{2}$的椭圆为“黄金椭圆”,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),e为椭圆E的离心率,则e2+e-1=0是椭圆E为“黄金椭圆”的( )| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 先求出方程e2+e-1=0的解,再结合充分必要条件的定义判断即可.
解答 解:∵椭圆的方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
解方程e2+e-1=0,解得:e=$\frac{\sqrt{5}-1}{2}$或e=-$\frac{\sqrt{5}+1}{2}$,
∴e2+e-1=0是椭圆E为“黄金椭圆”的必要不充分条件,
故选:C.
点评 本题考察了充分必要条件,考察转化思想问题,是一道基础题.

练习册系列答案
相关题目
20.与圆(x-2)2+y2=1相切且在两坐标轴上截距相等的直线共有( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 6条 |
4.已知m∈R,则函数f(x)=3x+m-2有零点的一个充分不必要条件为( )
| A. | 0<m<1 | B. | m<2 | C. | m<3 | D. | 0<m<3 |
4.已知|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=2,∠AOB=150°,点C在∠AOB的内部且∠AOC=30°,设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,则$\frac{m}{n}$=( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
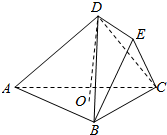 如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.
如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.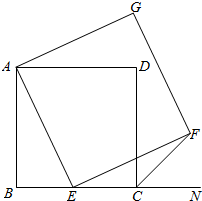 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.