题目内容
3.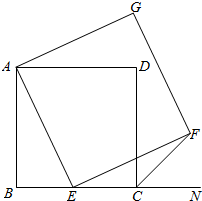 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.(1)连结GD,求证△ADG≌△ABE;
(2)连结FC,求证∠FCN=45°;
(3)请问在AB边上是否存在一点Q,使得四边形DQEF是平行四边形?若存在,请证明;若不存在,请说明理由.
分析 (1)由AB=AD,AE=AG,∠DAG=∠BAE推出三角形全等;
(2)过F作BN的垂线,设垂足为H,证明FH=CH即可.
(3)取AB中点Q,连结DQ,使用全等三角形得出AG与QD平行且相等,AG与EF平行且相等,故QD与EF平行且相等.
解答  证明:(1)如图,连接DG,
证明:(1)如图,连接DG,
∵四边形ABCD和四边形AEFG是正方形,
∴DA=BA,EA=GA,∠BAD=∠EAG=90°,
∴∠DAG=∠BAE,
∴△ADG≌△ABE;
(2)过F作BN的垂线,设垂足为H,
∵∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,
∴∠BAE=∠HEF,
∵AE=EF,
∴△ABE≌△EHF,
∴AB=EH,BE=FH,
∴AB=BC=EH,
∴BE+EC=EC+CH
∴CH=BE=FH,
∴∠FCN=45°;
(3)在AB上取AQ=BE,连接QD,
∵AB=AD,
∴△DAQ≌△ABE,
∵△ABE≌△EHF,
∴△DAQ≌△ABE≌△ADG,
∴∠GAD=∠ADQ,
∴AG、QD平行且相等,
又∵AG、EF平行且相等,
∴QD、EF平行且相等,
∴四边形DQEF是平行四边形,
∴在AB边上存在一点Q,使得四边形DQEF是,平行四边形.
点评 本题考查了全等三角形的判定与性质,平行四边形的判定,作出辅助线,找到全等三角形是关键.

练习册系列答案
相关题目
8.若f(x)=$\left\{\begin{array}{l}{lg(x-2),x>0}\\{{x}^{2}-1,x≤0}\end{array}\right.$,则函数y=f(x)的零点是3,-1.
9.定义:离心率e=$\frac{\sqrt{5}-1}{2}$的椭圆为“黄金椭圆”,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),e为椭圆E的离心率,则e2+e-1=0是椭圆E为“黄金椭圆”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
13.下列各表格中,不能看成y关于x的函数的是( )
| A. |
| B. |
| C. |
| D. |
|
12.设F1、F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左、右焦点,若椭圆上存在点A,使∠F1AF2=90°,且|AF1|=3|AF2|,则椭圆离心率为( )
| A. | $\frac{{\sqrt{5}}}{4}$ | B. | $\frac{{\sqrt{10}}}{4}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $\sqrt{5}$ |