题目内容
19.已知sin(2π-α)=$\frac{4}{5}$,α∈($\frac{3π}{2}$,2π),则$\frac{sinα+cosα}{sinα-cosα}$=$\frac{1}{7}$.分析 已知等式左边利用诱导公式化简,整理求出sinα的值,进而求出cosα的值,代入原式计算即可得到结果.
解答 解:∵sin(2π-α)=-sinα=$\frac{4}{5}$,即sinα=-$\frac{4}{5}$,α∈($\frac{3π}{2}$,2π),
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{3}{5}$,
则原式=$\frac{-\frac{4}{5}+\frac{3}{5}}{-\frac{4}{5}-\frac{3}{5}}$=$\frac{1}{7}$.
故答案为:$\frac{1}{7}$.
点评 此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
9.直线x+a2y+6=0与直线(a-2)x+3ay+2a=0平行,则实数a的值为( )
| A. | 3或-1 | B. | 0或-1 | C. | -3或-1 | D. | 0或3 |
7.已知点P(x,y)在圆x2+y2-4x-2y+4=0上,则$\frac{y}{x}$的最大值和最小值分别是( )
| A. | 1,$\frac{1}{3}$ | B. | $\frac{4}{3}$,0 | C. | $\frac{4}{3}$,-$\frac{4}{3}$ | D. | 2,2 |
14.若函数y=f(x)在x=a处的导数为A,则$\underset{lim}{△x→0}$$\frac{f(a+△x)-f(a-△x)}{△x}$为( )
| A. | A | B. | 2A | C. | $\frac{A}{2}$ | D. | 0 |
8.若f(x)=$\left\{\begin{array}{l}{lg(x-2),x>0}\\{{x}^{2}-1,x≤0}\end{array}\right.$,则函数y=f(x)的零点是3,-1.
9.定义:离心率e=$\frac{\sqrt{5}-1}{2}$的椭圆为“黄金椭圆”,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),e为椭圆E的离心率,则e2+e-1=0是椭圆E为“黄金椭圆”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
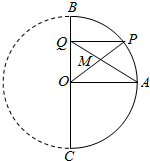 如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.
如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.