题目内容
4.若函数f(x)=2x-1,则f(3)=5.分析 利用函数性质求解.
解答 解:∵函数f(x)=2x-1,
∴f(3)=2×3-1=5.
故答案为:5.
点评 本题考查函数值的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
15.空间直角坐标系中,点A(-2,1,3)关于点B(1,-1,2)的对称点C的坐标为( )
| A. | (4,1,1) | B. | (-1,0,5) | C. | (4,-3,1) | D. | (-5,3,4) |
9.设x∈{-1,1},y∈{-2,0,2},则以(x,y)为坐标的点落在不等式x+2y≥1所表示的平面区域内的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
16.在正三棱柱ABC-A1B1C1中,已知AB=2,CC1=$\sqrt{2}$,则异面直线AB1和BC1所成角的余弦值为( )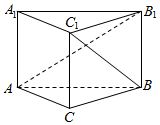

| A. | 0 | B. | $\frac{\sqrt{42}}{7}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
14.F为双曲线Г:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,若Г上存在一点P使得△OPF为等边三角形(O为坐标原点),则Г的离心率e为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{3}+1$ | D. | 2 |
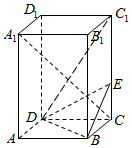 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.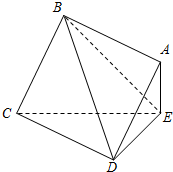 如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,
如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,