题目内容
16.在正三棱柱ABC-A1B1C1中,已知AB=2,CC1=$\sqrt{2}$,则异面直线AB1和BC1所成角的余弦值为( )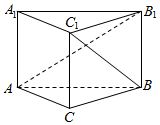
| A. | 0 | B. | $\frac{\sqrt{42}}{7}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
分析 连接B1C交BC1于E,连接DE,利用四边形BCC1B1是平行四边形及其三角形的中位线定理证明DE∥AB1,可得∠DEB或其补角为异面直线AB1与BC1所成的角,再利用余弦定理即可得出.
解答 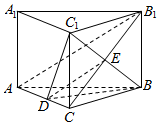 解:如图所示
解:如图所示
连接B1C交BC1于E,连接DE,
∵四边形BCC1B1是平行四边形,∴B1E=EC.
又AD=DC.
∴DE∥AB1,
∴∠DEB或其补角为异面直线AB1与BC1所成的角,
在△DEB中,DE=$\frac{\sqrt{6}}{2}$,BD=$\sqrt{3}$,BE=$\frac{\sqrt{6}}{2}$.
∴cos∠DEB=$\frac{\frac{6}{4}+\frac{6}{4}-3}{2•\frac{6}{4}•\frac{6}{4}}$=0,
∴异面直线AB1和BC1所成角的余弦值为0.
故选:A.
点评 本题考查了正三棱柱的性质、平行四边形的性质、三角形的中位线定理异面直线所成的角、余弦定理等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
6.在直角坐标系中,下列直线中倾斜角为钝角的是( )
| A. | y=3x-1 | B. | x+2=0 | C. | $\frac{x}{2}$+$\frac{y}{3}$=1 | D. | 2x-y+1=0 |
7.函数f(x)=3x-log2(-x)的零点所在区间是( )
| A. | $(-\frac{5}{2},-2)$ | B. | (-2,-1) | C. | (1,2) | D. | $(2,\frac{5}{2})$ |
11.从甲、乙、丙三人中任选两人参加社会实践活动,甲被选中的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
1.已知点A(0,0,0),B(1,0,1),C(0,1,1),则平面ABC的一个法向量$\overrightarrow m$是( )
| A. | (1,1,1) | B. | (1,1,-1) | C. | (-1,1,1) | D. | (1,-1,1) |
5.函数f(x)=x2(x-$\frac{2}{x}$)的导数为f′(x),则f′(1)等于( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |