题目内容
15.空间直角坐标系中,点A(-2,1,3)关于点B(1,-1,2)的对称点C的坐标为( )| A. | (4,1,1) | B. | (-1,0,5) | C. | (4,-3,1) | D. | (-5,3,4) |
分析 利用中点坐标公式求解.
解答 解:设C(x,y,z),
∵点A(-2,1,3)关于点B(1,-1,2)的对称点C,
∴$\left\{\begin{array}{l}{\frac{x-2}{2}=1}\\{\frac{y+1}{2}=-1}\\{\frac{z+3}{2}=2}\end{array}\right.$,解得x=4,y=-3,z=1,
∴C(4,-3,1).
故选:C.
点评 本题考查点的坐标的求法,是基础题,解题时要认真审题,注意中点坐标公式的合理运用.

练习册系列答案
相关题目
6.在直角坐标系中,下列直线中倾斜角为钝角的是( )
| A. | y=3x-1 | B. | x+2=0 | C. | $\frac{x}{2}$+$\frac{y}{3}$=1 | D. | 2x-y+1=0 |
20.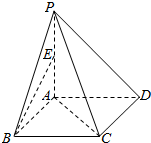 四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
 四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
7.函数f(x)=3x-log2(-x)的零点所在区间是( )
| A. | $(-\frac{5}{2},-2)$ | B. | (-2,-1) | C. | (1,2) | D. | $(2,\frac{5}{2})$ |
5.函数f(x)=x2(x-$\frac{2}{x}$)的导数为f′(x),则f′(1)等于( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |