题目内容
已知函数f(x)=x|x2-3|,x∈[0,m],其中m∈R,当函数f(x)的值域为[0,2]时,则实数m的取值范围 .
考点:函数的值域
专题:函数的性质及应用,导数的综合应用
分析:先去绝对值将函数f(x)变成:f(x)=
,通过求导判断函数x3-3x在[
,+∞)单调递增,并且令x3-3x=2得,x=2,因为f(x)的值域是[0,2],所以x≤2;同样的办法可判断函数3x-x3在[0,1]单调递增,在(1,
)单调递减,所以x=1时该函数取最大值2,x=0时取最小值0,所以函数f(x)在[0,1]上的值域是[0,2],并且x∈[0,2]时f(x)的值域也是[0,2],所以m∈[1,2].
|
| 3 |
| 3 |
解答:
解:f(x)=x|x2-3|=
;
(1)(x3-3x)′=3x2-3,∴x3-3x在[
,+∞)上单调递增,令x3-3x=2得,x=2,∴x∈[
,2];
(2)(3x-x3)′=3-3x2,∴3x-x3在[0,1)单调递增,在[1,
)上单调递减,∴x=1时3x-x3取最大值2,x=0时,取最小值0,即此时f(x)∈[0,2],∴x∈[0,
),且x∈[0,1]时f(x)的值域为[0,2];
∴x∈[0,1]f(x)值域是[0,2],x∈[0,2]时f(x)的值域也是[0,2];
∴m∈[1,2];
即实数m的取值范围为[1,2].
故答案为:[1,2].
|
(1)(x3-3x)′=3x2-3,∴x3-3x在[
| 3 |
| 3 |
(2)(3x-x3)′=3-3x2,∴3x-x3在[0,1)单调递增,在[1,
| 3 |
| 3 |
∴x∈[0,1]f(x)值域是[0,2],x∈[0,2]时f(x)的值域也是[0,2];
∴m∈[1,2];
即实数m的取值范围为[1,2].
故答案为:[1,2].
点评:考查处理含绝对值函数的方法,通过求导判断函数单调性的方法,以及函数单调性定义的应用,函数的值域的概念及函数最值的求法.

练习册系列答案
相关题目
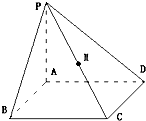 如图,四棱锥P-ABCD中,四边形ABCD是矩形,PA⊥平面ABCD,且AP=
如图,四棱锥P-ABCD中,四边形ABCD是矩形,PA⊥平面ABCD,且AP=