题目内容
关于x的不等式mx2-(m+3)x-1<0对于任意实数x均成立,则m的取值集合是 .
考点:一元二次不等式的应用
专题:
分析:分m=0、m≠0两种情况进行讨论:m=0时易检验;m≠0时,有
,解出即可得到.
|
解答:
解:当m=0时,不等式为-3x-1<0不恒成立;
当m≠0时,有
,
即
,解得-9<m<-1.
综上可得-9<m<-1.
故答案为:{m|-9<m<-1}
当m≠0时,有
|
即
|
综上可得-9<m<-1.
故答案为:{m|-9<m<-1}
点评:该题考查二次函数恒成立问题,考查学生分析解决问题的能力,属中档题.该题易忽略m=0时的情形.

练习册系列答案
相关题目
函数f(x)=3x-6的零点是( )
| A、0 | B、3 | C、2 | D、-6 |
下列各式错误的是( )
| A、30.8>30.7 | ||||
| B、0.75-0.1<0.750.1 | ||||
C、(
| ||||
| D、0.50.4>0.50.6 |
 如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF=2,∠BFC=90°,BF=FC,H为BC的中点.
如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF=2,∠BFC=90°,BF=FC,H为BC的中点.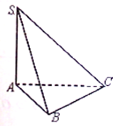 如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=2,BC=3,AB⊥BC,二面角S-BC-A为
如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=2,BC=3,AB⊥BC,二面角S-BC-A为