Question

设a∈R，函数f（x）=x|x-a|+2x．
（1）若a=2，求函数f（x）在区间[0，3]上的最大值；
（2）若a＞2，写出函数f（x）的单调区间（不必证明）；
（3）若存在a∈[3，6]，使得关于x的方程f（x）=t+2a有三个不相等的实数解，求实数t的取值范围．

Answer 1

考点：函数的最值及其几何意义,函数的零点与方程根的关系

专题：函数的性质及应用,导数的综合应用

分析：（1）根据图象可判断最大值．（2）分类讨论；①当x≥a时，f（x）=（x-

a-2

2

）²-

(a-2)2

4

．②当x＜a时，f（x）=-（x-

a-2

2

）²-

(a-2)2

4

．求解即可．
（3）求解关于x的方程f（x）=t+2a有三个不相等的实数解，根据单调性分类讨论求解．

解答： （1）当a=2，x∈[0，3]时，f（x）=x|x-2|=

x2，x≥2 -x2+4x，0≤x＜2

作函数图象，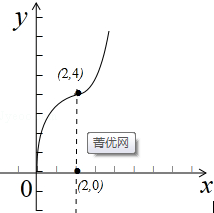

可知函数f（x）在区间[0，3]上是增函数．
所以f（x）在区间[0，3]上的最大值为f（3）=9．
（2）f（x）=

x2+(2-a)x，x≥a -x2+(2+a)x，x＜a

①当x≥a时，f（x）=（x-

a-2

2

）²-

(a-2)2

4

．
因为a＞2，所以

a-2

2

＜a．
所以f（x）在[a，+∞）上单调递增．
②当x＜a时，f（x）=-（x-

a-2

2

）²-

(a-2)2

4

．
因为a＞2，所以

a+2

2

＜a．
所以f（x）在（-∞，

a+2

2

]上单调递增，在[

a+2

2

，a]上单调递减．
综上所述，函数f（x）的递增区间是（-∞，

a+2

2

]和[a，+∞），递减区间是[

a+2

2

，a]．
（3）当3≤a≤6时，由（1）知f（x）在（-∞，

a+2

2

]，[a，+∞）上分别是增函数，
在[

a+2

2

，a]上是减函数，
当且仅当2a＜t+2a＜

(a+2)2

4

时，方程f（x）=t+2a有三个不相等的实数解．
即 0＜t＜

(a+2)2

4

令，g（a）=

(a-2)2

4

在a∈[3，6]时是增函数，
故g（a）_max=4．
∴实数t的取值范围是（0，4）．

点评：本题综合考查了函数的单调性，方程的根，函数的零点问题，属于难题．