Question

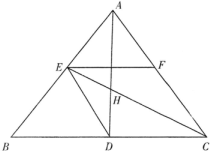如图，已知△ABC的两条角平分线AD和CE相交于H，B，E，H，D四点共圆，F在AC上，且∠DEC=∠FEC．
（I）求∠B的度数；
（Ⅱ）证明：AE=AF．

Answer 1

考点：平行线分线段成比例定理

专题：立体几何

分析：（I）由B，E，H，D四点共圆，可得∠CHD=∠B．再利用三角形的外角定理和三角形的内角和定理即可得出．
（II）利用四点共圆的性质、三角形的外角定理、三角形的内角和定理即可得出．

解答： （I）解：∵B，E，H，D四点共圆，∴∠CHD=∠B．
又∠CHD=∠HCA+∠HAC=

1

2

∠ACB+

1

2

∠CAB，
∴∠B=

1

2

∠ACB+

1

2

∠CAB，
∵∠B+∠ACB+∠CAB=180°，
∴3∠B=180°，
解得∠B=60°．
（II）证明：连接BH，
∵B，E，H，D四点共圆，
∴∠CHD=∠B，∠AEH=∠ADB．
∠DEH=∠BDH=

1

2

∠ABC=30°．
∵∠DEC=∠FEC，∴∠FEC=30°．
∴∠AFE=∠FCE+∠FEC=

1

2

∠ACB+30°．
∠AEF=∠ADB-30°
=∠ACB+∠DAC-30°
=∠ACB+

1

2

(180°-60°-∠ACB)-30°
=

1

2

∠ACB+30°．
∴∠AFE=∠AEF，
∴AE=AF．

点评：本题考查了四点共圆的性质、三角形的外角定理、三角形的内角和定理，考查了推理能力，属于中档题．