题目内容
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求f(x)的表达式;
(2)求直线y=
| 3 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)由f(x)=
,求得 sin(
x+
)=
,可得
x+
=2kπ+
,或
x+
=2kπ+
,k∈z,由此求得x的值,可得直线y=
与函数f(x)图象的所有交点的坐标.
(2)由f(x)=
| 3 |
| 1 |
| 2 |
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 4 |
| 2π |
| 3 |
| 3 |
解答:
解:(1)由函数的图象可得A=2,
=
•
=
-
,求得ω=
.
再根据五点法作图可得
•(-
)+φ=0,∴φ=
,∴f(x)=2sin(
x+
).
(2)由f(x)=2sin(
x+
)=
,求得 sin(
x+
)=
,∴
x+
=2kπ+
,或
x+
=2kπ+
,k∈z.
求得x=4kπ+
,或 x=4kπ+
,
故直线y=
与函数f(x)图象的所有交点的坐标为(4kπ+
,0),或(4kπ+
,0),k∈z.
| T |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| 3π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
再根据五点法作图可得
| 1 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
(2)由f(x)=2sin(
| 1 |
| 2 |
| π |
| 4 |
| 3 |
| 1 |
| 2 |
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 4 |
| 2π |
| 3 |
求得x=4kπ+
| π |
| 6 |
| 5π |
| 6 |
故直线y=
| 3 |
| π |
| 6 |
| 5π |
| 6 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,解三角方程,属于基础题.

练习册系列答案
相关题目
从1,2,3,4,5,6,7这七个数字中任取两个奇数和一个偶数,组成没有重复数字的三位数,其个数为( )
| A、432 | B、288 |
| C、216 | D、108 |
用反证法证明命题:“已知a,b∈N,若a,b能被5整除,则a,b中至少有一个能被5整除”时,反设正确的是( )
| A、a,b中有一个不能被5整除 |
| B、a,b中有一个能被5整除 |
| C、a,b都不能被5整除 |
| D、a,b都能被5整除 |
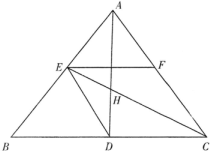 如图,已知△ABC的两条角平分线AD和CE相交于H,B,E,H,D四点共圆,F在AC上,且∠DEC=∠FEC.
如图,已知△ABC的两条角平分线AD和CE相交于H,B,E,H,D四点共圆,F在AC上,且∠DEC=∠FEC.