题目内容
已知函数f(x)=(ax+b)ex在x=0处取得极值,且函数f(x)的图象过点A(0,-1).
(1)求f(x)的解析式;
(2)设函数g(x)的定义域为D,若存在区间[m,n]⊆D,使得g(x)在[m,n]上的值域是[m+1,n+1],则称区间[m,n]为函数g(x)的“增值区间”.
①证明:当x>0,函数f(x)不存在“增值区间”;
②函数y=f(x)+2是否存在“增值区间”?若存在,写出一个“增值区间”(不必证明);若不存在,说明理由.
(1)求f(x)的解析式;
(2)设函数g(x)的定义域为D,若存在区间[m,n]⊆D,使得g(x)在[m,n]上的值域是[m+1,n+1],则称区间[m,n]为函数g(x)的“增值区间”.
①证明:当x>0,函数f(x)不存在“增值区间”;
②函数y=f(x)+2是否存在“增值区间”?若存在,写出一个“增值区间”(不必证明);若不存在,说明理由.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的概念及应用,导数的综合应用
分析:(1)由函数f(x)=(ax+b)ex在x=0处取得极值,且函数f(x)的图象过点A(0,-1).可得f′(0)=0,f(0)=-1,解方程组可得a,b的值,进而得到f(x)的解析式;
(2)①假设x>0时,函数f(x)存在增值区间[m,n],则方程(x-1)ex=x+1有两个不相等的正根,即函数h(x)=(x-1)ex-x-1在(0,+∞)上有两个不同的零点,利用导数法分析函数h(x)=(x-1)ex-x-1在(0,+∞)上仅有一个零点,与假设矛盾.可证得结论;②举出正例[0,1]是函数y=f(x)+2的一个“增值区间”.
(2)①假设x>0时,函数f(x)存在增值区间[m,n],则方程(x-1)ex=x+1有两个不相等的正根,即函数h(x)=(x-1)ex-x-1在(0,+∞)上有两个不同的零点,利用导数法分析函数h(x)=(x-1)ex-x-1在(0,+∞)上仅有一个零点,与假设矛盾.可证得结论;②举出正例[0,1]是函数y=f(x)+2的一个“增值区间”.
解答:
解:(1)∵f(x)=(ax+b)ex,
∴f′(x)=(ax+a+b)ex,…(1分)
∵函数f(x)=(ax+b)ex在x=0处取得极值,且函数f(x)的图象过点A(0,-1).
∴f′(0)=a+b=0,f(0)=b=-1,
解得:a=1,b=-1,
∴f(x)=(x-1)ex,…(4分)
证明:(2)①假设x>0时,函数f(x)存在增值区间[m,n].
∵x>0时,f′(x)=xex>0,
所以函数f(x)在区间(0,+∞)是增函数.…(5分)
∵函数f(x)存在增值区间[m,n],
则
,
问题转化为方程(x-1)ex=x+1有两个不相等的正根,
即函数h(x)=(x-1)ex-x-1在(0,+∞)上有两个不同的零点.…(7分)
又h′(x)=xex-1,
∵h′′(x)=(1+x)ex>0在(0,+∞)上恒成立,
∴h′(x)=xex-1在区间(0,+∞)上是增函数.…(8分)
∵h′(0)=-1<0,h′(1)=e-1>0,
∴在区间(0,1)存在x0使得h′(x0)=0,
∴当x∈(0,x0)时,h′(x)<0;当x∈(x0,+∞)时,h′(x)>0;,
∴h(x)=(x-1)ex-x-1在区间(0,x0)上是减函数,在区间(x0,+∞)上是增函数.…(10分)
∵h(x0)<h(0)=-2<0,
∴h(x)在区间(0,x0]上不存在零点.
而h(x0)•h(2)=(e3-3)h(x0)<0,
∴h(x)在区间(x0,+∞)上仅有一个零点,
故函数h(x)=(x-1)ex-x-1在(0,+∞)上仅有一个零点,与假设矛盾.
故当x>0时,不存在“增值区间”. …(12分)
解:②函数y=f(x)+2存在“增值区间”,…(13分)
[0,1]是它的一个“增值区间”.…(14分)
∴f′(x)=(ax+a+b)ex,…(1分)
∵函数f(x)=(ax+b)ex在x=0处取得极值,且函数f(x)的图象过点A(0,-1).
∴f′(0)=a+b=0,f(0)=b=-1,
解得:a=1,b=-1,
∴f(x)=(x-1)ex,…(4分)
证明:(2)①假设x>0时,函数f(x)存在增值区间[m,n].
∵x>0时,f′(x)=xex>0,
所以函数f(x)在区间(0,+∞)是增函数.…(5分)
∵函数f(x)存在增值区间[m,n],
则
|
问题转化为方程(x-1)ex=x+1有两个不相等的正根,
即函数h(x)=(x-1)ex-x-1在(0,+∞)上有两个不同的零点.…(7分)
又h′(x)=xex-1,
∵h′′(x)=(1+x)ex>0在(0,+∞)上恒成立,
∴h′(x)=xex-1在区间(0,+∞)上是增函数.…(8分)
∵h′(0)=-1<0,h′(1)=e-1>0,
∴在区间(0,1)存在x0使得h′(x0)=0,
∴当x∈(0,x0)时,h′(x)<0;当x∈(x0,+∞)时,h′(x)>0;,
∴h(x)=(x-1)ex-x-1在区间(0,x0)上是减函数,在区间(x0,+∞)上是增函数.…(10分)
∵h(x0)<h(0)=-2<0,
∴h(x)在区间(0,x0]上不存在零点.
而h(x0)•h(2)=(e3-3)h(x0)<0,
∴h(x)在区间(x0,+∞)上仅有一个零点,
故函数h(x)=(x-1)ex-x-1在(0,+∞)上仅有一个零点,与假设矛盾.
故当x>0时,不存在“增值区间”. …(12分)
解:②函数y=f(x)+2存在“增值区间”,…(13分)
[0,1]是它的一个“增值区间”.…(14分)
点评:本题考查的知识点是利用导数研究函数的极值,利用导数研究函数的单调性,运算量大,综合性强,转化过程复杂,属于难题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
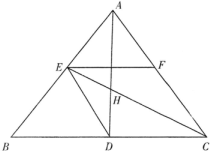 如图,已知△ABC的两条角平分线AD和CE相交于H,B,E,H,D四点共圆,F在AC上,且∠DEC=∠FEC.
如图,已知△ABC的两条角平分线AD和CE相交于H,B,E,H,D四点共圆,F在AC上,且∠DEC=∠FEC.