题目内容
下列各组向量中，可以作为基底的是（ ）
| A、（0，0）和（1，-2） | ||||
| B、（-1，2）和（5，7） | ||||
| C、（3，5）和（6，10） | ||||
D、（2，-3）和（
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：利用向量共线定理、共面向量基本定理即可判断出．
解答：
解：A．（0，0）和（1，-2）共线，因此不能作为基底；
B．（-1，2）和（5，7）不共线，可以作为基底；
C．（3，5）=
（6，10），共线不能作为基底；
D．（2，-3）=4（
，-
），共线不能作为基底．
综上可知：只有B满足条件．
故选：B．
B．（-1，2）和（5，7）不共线，可以作为基底；
C．（3，5）=
| 1 |
| 2 |
D．（2，-3）=4（
| 1 |
| 2 |
| 3 |
| 4 |
综上可知：只有B满足条件．
故选：B．
点评：本题考查了向量共线定理、共面向量基本定理，属于基础题．
练习册系列答案
相关题目
不等式（x+2y-1）（x-y+3）＞0所表示的平面区域为（ ）
A、 |
B、 |
C、 |
D、 |
甲、乙两人玩猜数字游戏，先由甲心中想一个数字，记为a，再由乙猜甲刚才所想的数字，把乙猜的数字记为b，其中a，b∈{0，1，2，3}，若|a-b|≤1，就称甲乙“心有灵犀”．现任意找两人玩这个游戏，则他们“心有灵犀”的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
用反证法证明命题：“已知a，b∈N，若a，b能被5整除，则a，b中至少有一个能被5整除”时，反设正确的是（ ）
| A、a，b中有一个不能被5整除 |
| B、a，b中有一个能被5整除 |
| C、a，b都不能被5整除 |
| D、a，b都能被5整除 |
已知∅表示空集，N表示自然数集，则下列关系式中，正确的是（ ）
| A、0∈∅ | B、∅⊆N |
| C、0⊆N | D、∅∈N |
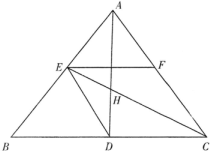如图，已知△ABC的两条角平分线AD和CE相交于H，B，E，H，D四点共圆，F在AC上，且∠DEC=∠FEC．