题目内容
由直线y=x+1上的一点向圆（x-2）2+（y-1）2=1引切线，则切线长的最小值为（ ）
A、
| ||
| B、1 | ||
C、
| ||
D、
|
考点：圆的切线方程
专题：直线与圆
分析：设直线y=x+1上任一点P（a，a+1），由点P向已知圆所引的切线长为m，点P到圆心的距离|PC|=
，由勾股定理，得（a-2）2+a2=1+m2=2（a-1）2+1，由此求出当a=1时，切线长m的最小值1．
| (a-2)2+a2 |
解答：
解：设直线y=x+1上任一点P（a，a+1），由点P向已知圆所引的切线长为m
由圆方程（x-3）2+（y-1）2=1可得其圆心在C（2，1），半径r=1
则点P到圆心的距离|PC|=
，
由勾股定理，得：|PC|2=r2+m2
（a-2）2+a2=1+m2
m2=2a2-4a+3
=2（a-1）2+1
则当a=1时，m2取得最小值为1，
所以此时切线长m的最小值为1．
故选：B．
由圆方程（x-3）2+（y-1）2=1可得其圆心在C（2，1），半径r=1
则点P到圆心的距离|PC|=
| (a-2)2+a2 |
由勾股定理，得：|PC|2=r2+m2
（a-2）2+a2=1+m2
m2=2a2-4a+3
=2（a-1）2+1
则当a=1时，m2取得最小值为1，
所以此时切线长m的最小值为1．
故选：B．
点评：本题考查圆的切线长的最小值的求法，是基础题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
函数y=lg（x+1）的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
sin（2014π）=（ ）
| A、-1 | ||||
| B、1 | ||||
C、
| ||||
| D、0 |
用反证法证明命题：“已知a，b∈N，若a，b能被5整除，则a，b中至少有一个能被5整除”时，反设正确的是（ ）
| A、a，b中有一个不能被5整除 |
| B、a，b中有一个能被5整除 |
| C、a，b都不能被5整除 |
| D、a，b都能被5整除 |
要得到y=
sin2x-cos2x的图象，可将函数y=4sinxcosx的图象（ ）
| 3 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
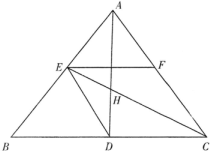如图，已知△ABC的两条角平分线AD和CE相交于H，B，E，H，D四点共圆，F在AC上，且∠DEC=∠FEC．