题目内容
 已知圆O:x2+y2=2交x轴于A、B两点,曲线C是以AB为长轴,离心率为
已知圆O:x2+y2=2交x轴于A、B两点,曲线C是以AB为长轴,离心率为
| ||
| 2 |
(Ⅰ) 求椭圆C的标准方程;
(Ⅱ) 若点P的坐标为(1,1)求证:直线PQ与圆O相切;
(Ⅲ) 试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由已知得a=
,e=
,由此能求出椭圆C的标准方程.
(Ⅱ)由已知得直线OQ的方程为y=-2x,从而点Q(-2,4),kOP⊥kPQ,由此能证明直线PQ与圆O相切.
(Ⅲ)当点P在圆O上运动时,直线PQ与圆O保持相切.设P(x0,y0),(x0≠±
),则y02=2-x02,直线OQ的方程为y=-
x,由此入手能证明直线PQ始终与圆O相切.
| 2 |
| ||
| 2 |
(Ⅱ)由已知得直线OQ的方程为y=-2x,从而点Q(-2,4),kOP⊥kPQ,由此能证明直线PQ与圆O相切.
(Ⅲ)当点P在圆O上运动时,直线PQ与圆O保持相切.设P(x0,y0),(x0≠±
| 2 |
| x0+1 |
| y0 |
解答:
(I)解:∵圆O:x2+y2=2交x轴于A、B两点,
曲线C是以AB为长轴,离心率为
的椭圆,
∴a=
,e=
,解得c=1,b=1,
∴椭圆C的标准方程为
+y2=1.…(4分)
(Ⅱ)证明:∵P(1,1),∴kPF=
,∴kOQ=-2,
∴直线OQ的方程为y=-2x,
∴点Q(-2,4)…(6分)
∴kPQ=-1,又kOP=1,∴kOP⊥kPQ,
即OP⊥PQ,故直线PQ与圆O相切.…(8分)
(Ⅲ)解:当点P在圆O上运动时,直线PQ与圆O保持相切,…(9分)
证明如下:设P(x0,y0),(x0≠±
),则y02=2-x02,
∴kPF=
,kOQ=-
,
∴直线OQ的方程为y=-
x,
∴点Q(-2,
),…(11分)
∴kPQ=
=
=
=-
,
又kOP=
,…(13分)
∴kOP•kPQ=-1,即OP⊥PQ,故直线PQ始终与圆O相切.…(14分)
曲线C是以AB为长轴,离心率为
| ||
| 2 |
∴a=
| 2 |
| ||
| 2 |
∴椭圆C的标准方程为
| x2 |
| 2 |
(Ⅱ)证明:∵P(1,1),∴kPF=
| 1 |
| 2 |
∴直线OQ的方程为y=-2x,
∴点Q(-2,4)…(6分)
∴kPQ=-1,又kOP=1,∴kOP⊥kPQ,
即OP⊥PQ,故直线PQ与圆O相切.…(8分)
(Ⅲ)解:当点P在圆O上运动时,直线PQ与圆O保持相切,…(9分)
证明如下:设P(x0,y0),(x0≠±
| 2 |
∴kPF=
| y0 |
| x0+1 |
| x0+1 |
| y0 |
∴直线OQ的方程为y=-
| x0+1 |
| y0 |
∴点Q(-2,
| 2x0+2 |
| y0 |
∴kPQ=
y0-
| ||
| x0+2 |
| y02-(2x0+2) |
| (x0+2)y0 |
=
| -x02-2x0 |
| (x0+2)y0 |
| x0 |
| y0 |
又kOP=
| y0 |
| x0 |
∴kOP•kPQ=-1,即OP⊥PQ,故直线PQ始终与圆O相切.…(14分)
点评:本题考查椭圆标准方程的求法,考查直线与圆相切的证明,考查直线与圆的位置关系的判断与证明,解题时要注意函数与方程思想的合理运用.

练习册系列答案
相关题目
以下四个命题中既是特称命题又是真命题的为( )
| A、锐角三角形的内角是锐角或钝角 | ||
B、存在一个负数x,使
| ||
| C、两个无理数的和必是无理数 | ||
| D、至少有一个实数x,使x2≤0 |
sin(2014π)=( )
| A、-1 | ||||
| B、1 | ||||
C、
| ||||
| D、0 |
要得到y=
sin2x-cos2x的图象,可将函数y=4sinxcosx的图象( )
| 3 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
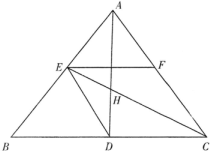 如图,已知△ABC的两条角平分线AD和CE相交于H,B,E,H,D四点共圆,F在AC上,且∠DEC=∠FEC.
如图,已知△ABC的两条角平分线AD和CE相交于H,B,E,H,D四点共圆,F在AC上,且∠DEC=∠FEC.