题目内容
函数y=tan（3x-
）的单调区间是（ ）
| π |
| 3 |
A、（-
| ||||||||
B、（-
| ||||||||
C、（-
| ||||||||
D、（-
|
考点：正切函数的图象
专题：计算题,三角函数的图像与性质
分析：利用正切函数的单调性，即可得出结论．
解答：
解：由题意，令（3x-
）∈（kπ-
，kπ+
）（k∈Z），
可得函数y=tan（3x-
）的单调区间是（-
+
，
+
）（k∈Z）．
故选：A．
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
可得函数y=tan（3x-
| π |
| 3 |
| π |
| 18 |
| kπ |
| 3 |
| 5π |
| 18 |
| kπ |
| 3 |
故选：A．
点评：本题考查正切函数的单调性，比较基础．
练习册系列答案
相关题目
随机变量X的概率分布规律为P（X=n）=
（n=1，2，3），其中a是常数，则P（
＜X＜
）的值为（ ）
| a |
| n(n+1) |
| 1 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
复数
•i2013（i是虚数单位）为纯虚数，则实数a的值为（ ）
| 2a+i |
| 1-2i |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
函数y=lg（x+1）的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
不等式（x+2y-1）（x-y+3）＞0所表示的平面区域为（ ）
A、 |
B、 |
C、 |
D、 |
以下四个命题中既是特称命题又是真命题的为（ ）
| A、锐角三角形的内角是锐角或钝角 | ||
B、存在一个负数x，使
| ||
| C、两个无理数的和必是无理数 | ||
| D、至少有一个实数x，使x2≤0 |
从1，2，3，4，5，6，7这七个数字中任取两个奇数和一个偶数，组成没有重复数字的三位数，其个数为（ ）
| A、432 | B、288 |
| C、216 | D、108 |
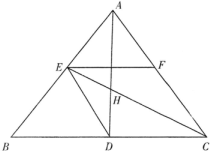如图，已知△ABC的两条角平分线AD和CE相交于H，B，E，H，D四点共圆，F在AC上，且∠DEC=∠FEC．