题目内容
已知定义在R上的函数f(x)是偶函数,对于任意x∈R,当x≥0都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-2013)+f(2014)的值为( )
| A、2 | B、1 | C、-1 | D、-2 |
考点:对数的运算性质
专题:函数的性质及应用
分析:由于函数f(x)是偶函数,可得f(-2013)=f(2013).又?x∈R都有f(x+2)=f(x).可得
f(-2013)+f(2014)=f(2013)+f(2014)=f(2×1012+1)+f(2×1013)=f(1)+f(0).
利用当x∈[0,2)时,f(x)=log2(x+1),可得f(1)+f(0)=log22+log21.即可得出.
f(-2013)+f(2014)=f(2013)+f(2014)=f(2×1012+1)+f(2×1013)=f(1)+f(0).
利用当x∈[0,2)时,f(x)=log2(x+1),可得f(1)+f(0)=log22+log21.即可得出.
解答:
解:∵函数f(x)是偶函数,
∴f(-2013)=f(2013).
又?x∈R都有f(x+2)=f(x).
∴f(-2013)+f(2014)=f(2013)+f(2014)=f(2×1012+1)+f(2×1013)=f(1)+f(0).
∵当x∈[0,2)时,f(x)=log2(x+1),
∴f(1)+f(0)=log22+log21=1.
∴f(-2013)+f(2014)=1.
故选:B.
∴f(-2013)=f(2013).
又?x∈R都有f(x+2)=f(x).
∴f(-2013)+f(2014)=f(2013)+f(2014)=f(2×1012+1)+f(2×1013)=f(1)+f(0).
∵当x∈[0,2)时,f(x)=log2(x+1),
∴f(1)+f(0)=log22+log21=1.
∴f(-2013)+f(2014)=1.
故选:B.
点评:本题考查了函数的奇偶性、周期性、函数值的计算,属于中档题.

练习册系列答案
相关题目
一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
| A、57.2 3.6 |
| B、57.2 |
| C、62.8 63.6 |
| D、62.8 3.6 |
已知x,y满足(x-1)2+y2=16,则x2+y2的最小值为( )
| A、3 | B、5 | C、9 | D、25 |
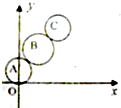 我们把圆心在一条直线上且相邻两圆彼此外切的一组圆 叫做“串圆”.在如图所示的“串圆”中,⊙A和⊙C的方程分别为x2+(y-1)2=2和(x-6)2+(y-7)2=2,则⊙B的方程为
我们把圆心在一条直线上且相邻两圆彼此外切的一组圆 叫做“串圆”.在如图所示的“串圆”中,⊙A和⊙C的方程分别为x2+(y-1)2=2和(x-6)2+(y-7)2=2,则⊙B的方程为