题目内容
某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望E(X).
| 围棋社 | 舞蹈社 | 拳击社 | |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望E(X).
考点:离散型随机变量及其分布列,古典概型及其概率计算公式,离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)先根据分层抽样的特点求出m的值,然后利用古典概型及其概率计算公式进行求解即可;
(Ⅱ)由题意可知:X=0,1,2,然后根据古典概型及其概率计算公式分别求出相应的概率,写出分布列,最后利用数学期望公式解之即可.
(Ⅱ)由题意可知:X=0,1,2,然后根据古典概型及其概率计算公式分别求出相应的概率,写出分布列,最后利用数学期望公式解之即可.
解答:
解:(Ⅰ)由于按分层抽样的方法从三个社团成员中抽取18人,拳击社被抽出了6人,
∴
=
,
∴m=2,
设A=“拳击社团被抽出的6人中有5人是男生”,
∴P(A)=
=
;
(Ⅱ)由题意可知:X=0,1,2,
P(X=0)=
=
,P(X=1)=
=
P(X=2)=
=
=
,
∴E(X)=0×
+1×
+2×
=
.
∴
| 6 |
| 28+m |
| 18 |
| 20+40+28+m |
∴m=2,
设A=“拳击社团被抽出的6人中有5人是男生”,
∴P(A)=
| ||||
|
| 48 |
| 145 |
(Ⅱ)由题意可知:X=0,1,2,
P(X=0)=
| ||
|
| 92 |
| 145 |
| ||||
|
| 48 |
| 145 |
| ||||
|
| 5 |
| 145 |
| 1 |
| 29 |
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 92 |
| 145 |
| 48 |
| 145 |
| 1 |
| 29 |
| 58 |
| 145 |
点评:本题主要考查了古典概型及其概率计算公式,以及离散型随机变量及其分布列和期望,同时考查了分析问题的能力和运算求解的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
直线2x-3y-3=0在x轴上的截距为( )
A、-
| ||
| B、-1 | ||
C、
| ||
| D、3 |
已知定义在R上的函数f(x)是偶函数,对于任意x∈R,当x≥0都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-2013)+f(2014)的值为( )
| A、2 | B、1 | C、-1 | D、-2 |
 一组数据如茎叶图所示,则这组数据的中位数和平均数分别是( )
一组数据如茎叶图所示,则这组数据的中位数和平均数分别是( )| A、11.5和12 |
| B、11.5和11.5 |
| C、11和11.5 |
| D、12和12 |
已知函数f(x)=
,则f[f(
)]等于( )
|
| 5 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
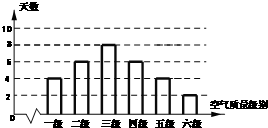 根据空气质量指数AQI(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数AQI(为整数)的不同,可将空气质量分级如下表: