题目内容
已知在△ABC中，a=
，b=
，A=30°，求c．
| 5 |
| 15 |
考点：正弦定理的应用
专题：解三角形
分析：首先利用正弦定理求出B的大小，然后根据三角形的边角知识，对三角形的解的情况进行分类讨论．
解答：
解：由正弦定理得sinB=
=
=
，
又∵b＞a，
∴B＞A，所以B=60°或120°
（1）当B=60°时，C=90°
根据勾股定理得：
∴c=
=2
，
（2）当B=120°时，C=A=30°
∴c=a=
，
综上可知：c=
或2
故答案为：c=
或2
| bsinA |
| a |
| ||
|
| ||
| 2 |
又∵b＞a，
∴B＞A，所以B=60°或120°
（1）当B=60°时，C=90°
根据勾股定理得：
∴c=
| a2+b2 |
| 5 |
（2）当B=120°时，C=A=30°
∴c=a=
| 5 |
综上可知：c=
| 5 |
| 5 |
故答案为：c=
| 5 |
| 5 |
点评：本题考查的知识点：正弦定理在解三角形中的应用，根据三角形解的情况进行分类讨论及相关的运算问题．
练习册系列答案
阅读快车系列答案
相关题目
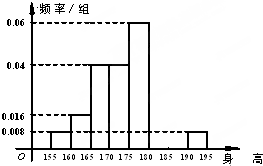从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，右图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．
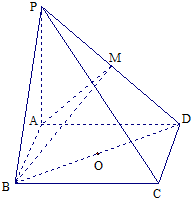如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以BD的中点O为球心、BD为直径的球面交PD于点M．直线2014x-y=0被圆x2+y2=1截得的弦长为（ ）
A、
| ||
| B、1 | ||
| C、4 | ||
| D、2 |
下列说法中正确的是（ ）
| A、一个命题的逆命题为真，则它的逆否命题一定为真 |
| B、“a＞b”与“a+c＞b+c”不等价 |
| C、“a2+b2=0，则a，b全为0”的逆否命题是“若a，b全不为0，则a2+b2≠0” |
| D、一个命题的否命题为真，则它的逆命题一定为真 |
若f（x）是奇函数，且x0是函数y=f（x）-ex的一个零点，则-x0一定是下列哪个函数的零点（ ）
| A、y=f（-x）ex-1 |
| B、y=f（x）e-x+1 |
| C、y=f（x）ex+1 |
| D、y=f（x）ex-1 |