题目内容
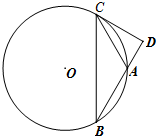
【几何证明选讲选做题】如图，过点C作△ABC的外接圆O的切线交BA的延长线 于点D．若CD=
| 3 |
考点：弦切角
专题：解三角形
分析：利用切割线定理求出DA，DB，再证明△DAC∽△DCB，即可得出结论．
解答：
解：由CD是圆的切线，可得CD2=DA×DB=DA×（DA+AB）．
∵CD=
，AB=2，
∴DA2+2DA-3=0，解得DA=1，DB=3．
∵∠DCA=∠DBC，∠ADC=∠CDB，
∴△DAC∽△DCB，
∴
=
∴BC=
=2
．
故答案为：2
．
∵CD=
| 3 |
∴DA2+2DA-3=0，解得DA=1，DB=3．
∵∠DCA=∠DBC，∠ADC=∠CDB，
∴△DAC∽△DCB，
∴
| AC |
| BC |
| CD |
| BD |
∴BC=
| AC×BD |
| CD |
| 3 |
故答案为：2
| 3 |
点评：本题考查切割线定理的运用，考查三角形相似的证明与运用，考查学生分析解决问题的能力，确定三角形相似是关键．
练习册系列答案
相关题目
若log4x=1，则
的值为（ ）
| x |
| A、2 | B、±2 | C、0 | D、4 |
连掷两次骰子得到的点数分别为m和n，若记向量
=（m，n）与向量
=（1，-2）的夹角为θ，则θ为锐角的概率是（ ）
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
将八进制数131（8）化为二进制数为（ ）
| A、1011001（2） |
| B、1001101（2） |
| C、1000011（2） |
| D、1100001（2） |