题目内容
求证:
-
cos2x+
cos4x=sin4x.
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:从等式的左边入手,借助于三角恒等变换公式进行求解.
解答:
证明:左边=
-
cos2x+
cos4x
=
-
cos2x+
(2cos22x-1)
=
-
cos2x+
cos22x-
=
-
(2cos2x-1)+
cos22x
=
-cos2x+
+
cos22x
=
-cos2x+
(2cos2x-1)2
=
-(1-sin2x)+
[2(1-sin2x)-1)2
=sin4x=右边,
∴
-
cos2x+
cos4x=sin4x.
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
=
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
=
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
=
| 3 |
| 4 |
| 1 |
| 4 |
=
| 3 |
| 4 |
| 1 |
| 4 |
=sin4x=右边,
∴
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
点评:本题重点考查了三角恒等变换、三角公式、同角三角函数基本关系式等知识,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
执行如图的程序框图,那么输出的S=( )


| A、720 | B、120 |
| C、24 | D、-120 |
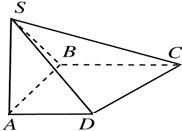 如图所示,ABCD是直角梯形,∠ABC=90°,SA⊥底面ABCD,SA=AB=BC=1,AD=
如图所示,ABCD是直角梯形,∠ABC=90°,SA⊥底面ABCD,SA=AB=BC=1,AD=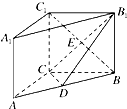 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是线段AB上的一点,且∠CDB1=90°,AA1=CD,则点A1到平面B1CD的距离为
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是线段AB上的一点,且∠CDB1=90°,AA1=CD,则点A1到平面B1CD的距离为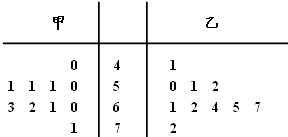 随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图:
随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图: