题目内容
3．已知条件p：（x-m）（x-m-3）＞0；条件q：x2+3x-4＜0．若p是q的必要不充分条件，则实数m的取值范围是（ ）| A． | （-∞，-7）∪（1，+∞） | B． | （-∞，-7]∪[1，+∞） | C． | （-7，1） | D． | [-7，1] |
分析 分别解出p，q的不等式，根据p是q的必要不充分条件，即可得出．
解答 解：条件p：（x-m）（x-m-3）＞0；解得：m+3＜x，或x＜m．
条件q：x2+3x-4＜0．解得-4＜x＜1，
∵p是q的必要不充分条件，∴1≤m，或m+3≤-4，解得m≥1或m≤-7．
则实数m的取值范围是（-∞，-7]∪[1，+∞）．
故选：B．
点评 本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
13．设点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的右支上，双曲线的左、右焦点分别为F1，F2，若|PF1|=4|PF2|，则双曲线离心率的取值范围是（ ）
| A． | $（{1，\frac{5}{3}}]$ | B． | （1，2] | C． | $[{\frac{5}{3}，+∞}）$ | D． | [2，+∞） |
11．设f（x）=|sinπx|，则f（1）+f（2）+f（3）+…+f（2010）=（ ）
| A． | 0 | B． | $\sqrt{3}$ | C． | -$\sqrt{3}$ | D． | 1 |
8．已知双曲线C：$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的焦点到渐近线的距离为3，则双曲线C的虚轴长为（ ）
| A． | 3 | B． | 6 | C． | $2\sqrt{5}$ | D． | $2\sqrt{21}$ |
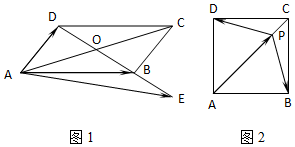（1）如图1，在平行四边形ABCD中，点E是对角线DB的延长线上一点，且OB=BE．记$\overrightarrow{AB}=\overrightarrow a\;，\;\overrightarrow{AD}=\overrightarrow b$，试用向量$\overrightarrow a\;，\;\overrightarrow b$表示$\overrightarrow{AE}$．