题目内容
15.两个好朋友相约周天在9点到10点到银川市图书馆看书,先到者等候另一个人20分钟方可离去.试求这两人能会面的概率?分析 由题意知本题是一个几何概型,试验包含的所有事件是Ω={(X,Y)|0≤X≤60,0≤Y≤60},做出事件对应的集合表示的面积,
写出满足条件的事件是A={(X,Y)||X-Y|≤20},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果
解答 解:以X、Y分别表示两人到达时刻,建立直角坐标系如图:
则0≤X≤60,0≤Y≤60.两人能会面的充要条件是|X-Y|≤20,
由题意找出会面的区域,以X、Y分别表示两人到达时刻,建立直角坐标系如图: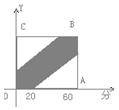
则0≤X≤60,0≤Y≤60.两人能会面的充要条件是|X-Y|≤20
∴P=$\frac{S_阴}{{{S_{OABC}}}}=\frac{{{{60}^2}-(60-20{)^2}}}{{{{60}^2}}}=\frac{5}{9}$.
点评 本题考查了几何概型求概率,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
5.已知集合A={x|x2+2x<0},B={x|($\frac{1}{2}$)x-2≥0},则A∩B=( )
| A. | (-2,-1) | B. | (-1,0) | C. | (-2,-1] | D. | [-1,0) |
3.已知条件p:(x-m)(x-m-3)>0;条件q:x2+3x-4<0.若p是q的必要不充分条件,则实数m的取值范围是( )
| A. | (-∞,-7)∪(1,+∞) | B. | (-∞,-7]∪[1,+∞) | C. | (-7,1) | D. | [-7,1] |
5.若p是真命题,q是假命题,则( )
| A. | p且q是真命题 | B. | p或q是假命题 | C. | 非p是真命题 | D. | 非q是真命题 |