Question

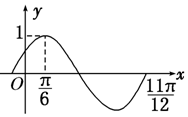
18．函数f（x）=3sin （2x-$\frac{π}{3}$） 的图象为C．
①图象C关于直线x=$\frac{11}{12}$π对称；
②函数f（x）在区间（-$\frac{π}{12}$，$\frac{5π}{12}$） 内是增函数；
③由y=3sin 2x的图象向右平移$\frac{π}{3}$个单位长度可以得到图象C．
以上三个论断中，正确论断的个数是（　　）

• A． 0个
• B． 1个
• C． 2个
• D． 3个

Answer 1

分析 ①②由三角函数图象的对称性和单调性判断即可；
③根据图象的平移可得．

解答 解：函数f（x）=3sin （2x-$\frac{π}{3}$） 的图象为C．
①f（$\frac{11}{12}$π）=-3，故x=$\frac{11}{12}$π是函数的一条称对称轴，故正确；
②函数f（x）的增区间为[kπ-$\frac{π}{12}$，kπ+$\frac{5π}{12}$]，故在区间（-$\frac{π}{12}$，$\frac{5π}{12}$） 内是增函数，故正确；
③由y=3sin 2x的图象向右平移$\frac{π}{3}$个单位长度可以得到图象y=3sin2（x-$\frac{π}{3}$）的图象，故错误．
故选C．

点评 考查了三角函数图象的对称性，单调性和函数图象的平移．属于基础题型，应熟练掌握．