题目内容
已知函数f(x)=
loga(ax)•loga(a2x)(a>0,且a≠1).
(1)解关于x的不等式f(x)>0;
(2)若函数f(x)在[2,8]上的最大值是1,最小值是-
,求a的值.
| 1 |
| 2 |
(1)解关于x的不等式f(x)>0;
(2)若函数f(x)在[2,8]上的最大值是1,最小值是-
| 1 |
| 8 |
考点:利用导数求闭区间上函数的最值,对数的运算性质,指、对数不等式的解法
专题:函数的性质及应用
分析:(1)先将不等式进行化简,转化为关于logax的二次不等式,解出logax后,再结合已知求解x的范围;
(2)利用换元思想,将问题转化为二次函数在指定区间上的最值问题,结合配方法求出结果,注意分类讨论.
(2)利用换元思想,将问题转化为二次函数在指定区间上的最值问题,结合配方法求出结果,注意分类讨论.
解答:
解:(1)f(x)=
(logax+1)(logax+2)=
(log
x+3logax+2),
令f(x)>0,即log
x+3logax+2>0,解得log2x<-2或logax>-1,
当0<a<1时,不等式解集为{x|0<x<
或x>
},
当a>1时,不等式解集为{x|0<x<
或x>
},
(2)由题意知f(x)=
(logax+1)(logax+2)
=
(loga2x+3logax+2)=
(logax+
)2-
.
当f(x)取最小值-
时,logax=-
.
又∵x∈[2,8],∴a∈(0,1).
∵f(x)是关于logax的二次函数,
∴函数f(x)的最大值必在x=2或x=8时取得.
若
(loga2+
)2-
=1,则a=2-
,
此时f(x)取得最小值时,x=(2-
)-
=
∉[2,8],舍去.
若
(loga8+
)2-
=1,则a=
,
此时f(x)取得最小值时,x=(
)-
=2
∈[2,8],
符合题意,∴a=
.
| 1 |
| 2 |
| 1 |
| 2 |
2 a |
令f(x)>0,即log
2 a |
当0<a<1时,不等式解集为{x|0<x<
| 1 |
| a |
| 1 |
| a2 |
当a>1时,不等式解集为{x|0<x<
| 1 |
| a2 |
| 1 |
| a |
(2)由题意知f(x)=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
当f(x)取最小值-
| 1 |
| 8 |
| 3 |
| 2 |
又∵x∈[2,8],∴a∈(0,1).
∵f(x)是关于logax的二次函数,
∴函数f(x)的最大值必在x=2或x=8时取得.
若
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
| 1 |
| 3 |
此时f(x)取得最小值时,x=(2-
| 1 |
| 3 |
| 3 |
| 2 |
| 2 |
若
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
此时f(x)取得最小值时,x=(
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
符合题意,∴a=
| 1 |
| 2 |
点评:对数函数与二次函数复合构成的函数,对数函数为内层时,一般采用换元法转化为二次函数来求解,注意中间量的取值范围.

练习册系列答案
相关题目
已知:A={x|x2=1},B={x|ax=1},C={x|x=a},B⊆A,则C的真子集个数是( )
| A、3 | B、6 | C、7 | D、8 |
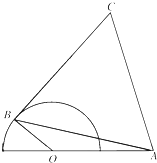 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.