题目内容
求作一个方程,使它的根是方程x2-7x+8=0的两根的平方的负倒数.
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:设x1.x2为方程x2-7x+8=0的两根,则-
,-
为所求方程的两根,求出(-
)(-
)=
,(-
)+(-
)=-
,从而得出方程.
| 1 |
| x12 |
| 1 |
| x22 |
| 1 |
| x12 |
| 1 |
| x22 |
| 1 |
| 64 |
| 1 |
| x12 |
| 1 |
| x22 |
| 33 |
| 64 |
解答:
解:设x1.x2为方程x2-7x+8=0的两根,
则-
,-
为所求方程的两根,有x1+x2=7,x1x2=8;
∴(-
)(-
)=
=
,
(-
)+(-
)=-
=-
=-
,
所以所求方程为
x2+
x+
=0
即64x2+33x+1=0
则-
| 1 |
| x12 |
| 1 |
| x22 |
∴(-
| 1 |
| x12 |
| 1 |
| x22 |
| 1 |
| (x1•x2)2 |
| 1 |
| 64 |
(-
| 1 |
| x12 |
| 1 |
| x22 |
| (x1+x2)2-2x1x2 |
| (x1•x2)2 |
| 49-16 |
| 64 |
| 33 |
| 64 |
所以所求方程为
x2+
| 33 |
| 64 |
| 1 |
| 64 |
即64x2+33x+1=0
点评:本题考查了函数的零点与方程的根的关系,考查韦达定理,是一道基础题.

练习册系列答案
相关题目
若集合A={0,1,2,3,4},B={1,2,4}则A∪B=( )
| A、{0,1,2,3,4} |
| B、{1,2,3,4} |
| C、{1,2} |
| D、{0} |
M是椭圆
+
=1上的点,F1、F2是椭圆的两个焦点,∠F1MF2=60°,则△F1MF2的面积等于( )
| x2 |
| 25 |
| y2 |
| 9 |
A、3
| ||
B、6
| ||
| C、3 | ||
D、2
|
椭圆
+
=1(a>b>0)的两个焦点是F1、F2,以|F1F2|为斜边作等腰直角三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
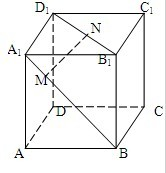 如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.
如图,在正方体ABCD-A1B1C1D1中,点N在线段B1D1上,且D1N=2NB1,点M在线段A1B上,且BM=2MA1.求证:MN∥平面AC1B.