题目内容
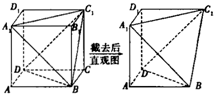
如图所示,用过A1、B、C1和C1、B、D的两个截面截去正方体ABCD-A1B1C1D1的两个角后得到一个新的几何体,则该几何体的正视图为( )

A、 |
B、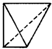 |
C、 |
D、 |
考点:简单空间图形的三视图
专题:计算题,空间位置关系与距离
分析:直接利用三视图的定义,正视图是光线从几何体的前面向后面正投影得到的投影图,据此可以判断出其正视图.
解答:
解:由正视图的定义可知:点A、A1、C1在后面的投影点分别是点D、D1、C1,线段A1B在后面的投影面上的投影是以D1为端点且与线段A1B平行且相等的线段,即可得正视图.
故选:A.
故选:A.
点评:从正视图的定义可以判断出题中的正视图,同时要注意能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.

练习册系列答案
相关题目
使函数y=2sin(2x+φ+
)为奇函数,且在[0,
]上是减函数的φ的一个值是( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p:当0<x<2时x2<4,命题q:当b<a<0时b2<a2,则( )
| A、p∧(¬q)为真 |
| B、p∧q为真 |
| C、(¬p)∨q为真 |
| D、(¬p)∧q为真 |
已知函数f(x)=1+2
sinxcosx-2
sin2x,x∈R.
(1)求函数f(x)的单调增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=3,b=
,f(A)=1,求角C.
| 3 |
| 3 |
(1)求函数f(x)的单调增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=3,b=
| 3 |
已知点P在圆C:x2+y2=2x+2y上,则点P到直线l:x+y+1=0的距离最大值为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、3
|