题目内容
| ∫ |
-
|
| 1 |
| 4 |
考点:微积分基本定理
专题:计算题,导数的概念及应用
分析:求出原函数,即可求得定积分.
解答:
解:
(cosx+
x3+1)dx=(sinx+
x4+x)
=
+
•(
)4+
+
-
•(
)4+
=
+
.
故答案为:
+
.
| ∫ |
-
|
| 1 |
| 4 |
| 1 |
| 16 |
| | |
-
|
| ||
| 2 |
| 1 |
| 16 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 1 |
| 16 |
| π |
| 4 |
| π |
| 4 |
=
| 2 |
| π |
| 2 |
故答案为:
| 2 |
| π |
| 2 |
点评:此题考查学生掌握函数的求导法则,会求函数的定积分运算,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
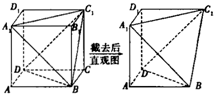
在每条棱长都相等的底面是菱形的直棱柱ABCD-A1B1C1D1中,∠ABC=
,侧棱AA1与对角线BD1所成的角为θ,则θ为( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
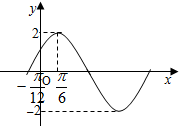 已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)的一部分图象如图所示,(其中A>0,ω>0,|φ|<