题目内容
在平面内,设A,B为两个定点,且AB=3,动点M满足
=2,则AM的最大值为 .
| MA |
| MB |
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立直角坐标系.设A(-
,0),B(
,0),M(x,y).由于动点M满足
=2,可得
=2,化为:(x-
)2+y2=4.可得圆心C,半径r.可得|AM|的最大值为|AC|+r.
| 3 |
| 2 |
| 3 |
| 2 |
| MA |
| MB |
| ||||
|
| 5 |
| 2 |
解答:
解:以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立直角坐标系.
设A(-
,0),B(
,0),M(x,y).
∵动点M满足
=2,
∴
=2,
化为:(x-
)2+y2=4.
圆心为C(
,0),半径r=2.
因此|AM|的最大值为|AC|+r=
-(-
)+2=6.
故答案为:6.
设A(-
| 3 |
| 2 |
| 3 |
| 2 |
∵动点M满足
| MA |
| MB |
∴
| ||||
|
化为:(x-
| 5 |
| 2 |
圆心为C(
| 5 |
| 2 |
因此|AM|的最大值为|AC|+r=
| 5 |
| 2 |
| 3 |
| 2 |
故答案为:6.
点评:本题考查了通过建立适当的坐标系求点的轨迹的方法,考查了两点之间的距离公式、点与圆的位置关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知{an}是等差数列,其前n项和为Sn,若a4+a5=20,则S8=( )
| A、18 | B、36 | C、64 | D、80 |
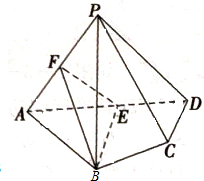 四棱锥P-ABCD中,AB=AD,∠BAD=60°,CD⊥AD,F,E分别是PA,AD的中点,求证:平面PCD∥平面FEB.
四棱锥P-ABCD中,AB=AD,∠BAD=60°,CD⊥AD,F,E分别是PA,AD的中点,求证:平面PCD∥平面FEB.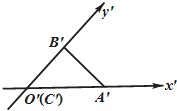 水平放置的△ABC由“斜二测画法”画得的直观图如图所示,已知A′C′=3,B′C′=2,则AB边的实际长度为( )
水平放置的△ABC由“斜二测画法”画得的直观图如图所示,已知A′C′=3,B′C′=2,则AB边的实际长度为( )