Question

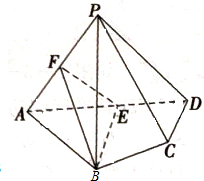四棱锥P-ABCD中，AB=AD，∠BAD=60°，CD⊥AD，F，E分别是PA，AD的中点，求证：平面PCD∥平面FEB．

Answer 1

考点：平面与平面平行的判定

专题：证明题,空间位置关系与距离

分析：证明平面PCD∥平面FEB，只需证明直线EF∥平面PCD，直线BE∥平面PCD，即可得出结论．

解答： 证明：在△PAD中，因为E，F分别为AP，AD的中点，所以EF∥PD．
又因为EF不在平面PCD中，PD?平面PCD
所以直线EF∥平面PCD．
因为AB=AD，∠BAD=60°，E是AD的中点，
所以BE⊥AD，
因为CD⊥AD，
所以BE∥CD，
因为BE不在平面PCD中，CD?平面PCD
所以直线BE∥平面PCD．
因为EF∩BE=E，
所以平面PCD∥平面FEB．

点评：本题考查平面与平面平行，考查学生分析解决问题的能力，证明直线EF∥平面PCD，直线BE∥平面PCD是关键．