题目内容
等差数列{an}公差不为0,且a2a4a9成等比数列.an的前项和为Sn且 S7=70.
(1)求{an}的通项公式
(2)若bn=
求的前项和Tn.
(1)求{an}的通项公式
(2)若bn=
| 1 |
| an•an+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列的通项公式、前n项和公式和等比数列性质,能求出an=3n-2.
(2)由bn=
=
=
(
-
),利用裂项求和法能求出bn=
求的前项和Tn.
(2)由bn=
| 1 |
| an•an+1 |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
| 1 |
| an•an+1 |
解答:
解:(1)∵等差数列{an}公差不为0,且a2a4a9成等比数列,
an的前项和为Sn且 S7=70,
∴
,
由d≠0,得a1=1,d=3,
∴an=1+(n-1)×3=3n-2.
(2)bn=
=
=
(
-
)
∴Tn=
(1-
+
-
+…+
-
)
=
(1-
)
=
.
an的前项和为Sn且 S7=70,
∴
|
由d≠0,得a1=1,d=3,
∴an=1+(n-1)×3=3n-2.
(2)bn=
| 1 |
| an•an+1 |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
∴Tn=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
=
| 1 |
| 3 |
| 1 |
| 3n+1 |
=
| n |
| 3n+1 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
△ABC中,sinA:sinB:sinC=4:7:8,则△ABC一定为( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
已知f(x)是可导的函数,且f′(x)<f(x)对于x∈R恒成立,则( )
| A、f(1)<ef(0),f(2015)>e2015f(0) |
| B、f(1)>ef(0),f(2015)>e2015f(0) |
| C、f(1)>ef(0),f(2015)<e2015f(0) |
| D、f(1)<ef(0),f(2015)<e2015f(0) |
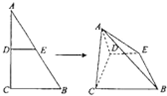 直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.
直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.