题目内容
已知f（x）是可导的函数，且f′（x）＜f（x）对于x∈R恒成立，则（ ）
| A、f（1）＜ef（0），f（2015）＞e2015f（0） |
| B、f（1）＞ef（0），f（2015）＞e2015f（0） |
| C、f（1）＞ef（0），f（2015）＜e2015f（0） |
| D、f（1）＜ef（0），f（2015）＜e2015f（0） |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：构造函数令h(x)=
，利用判断及单调性即可判断．
| f(x) |
| ex |
解答：
解：令h(x)=
，则h′(x)=
=
，
由于f'（x）＜f（x），ex＞0对于x∈R恒成立，
所以h'（x）＜0在R上恒成立，
所以h(x)=
为减函数，
∴
＜
，
即f（x）＜ef（0）；
＜
，
即f（2015）＜e2015f（0）．
故选：D
| f(x) |
| ex |
| f′(x)ex-f(x)ex |
| (ex)2 |
| f′(x)-f(x) |
| ex |
由于f'（x）＜f（x），ex＞0对于x∈R恒成立，
所以h'（x）＜0在R上恒成立，
所以h(x)=
| f(x) |
| ex |
∴
| f(1) |
| e |
| f(0) |
| e0 |
即f（x）＜ef（0）；
| f(2015) |
| e2015 |
| f(0) |
| e0 |
即f（2015）＜e2015f（0）．
故选：D
点评：本题主要考查了导数和函数的单调性的关系，关键是构造函数，属于中档题．
练习册系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，直线AB1与BC1所成角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |
双曲线
-y2=1的渐近线方程为（ ）
| x2 |
| 4 |
A、y=±
| ||
| B、y=±x | ||
| C、y=±2x | ||
| D、y=±4x |
在正三棱柱中，AB=AA1=1，P在平面ABC内运动，使得三角形AC1P的面积为
，则动点P的轨迹是（ ）
| 1 |
| 2 |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
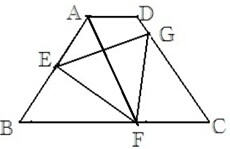如图，梯形ABCD，AD∥BC，AB=CD=6，AD=2，BC=8，∠B=60°，点E在AB上，点F在BC上，