题目内容
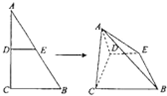 直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.
直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.(Ⅰ)求证:面ADC⊥面ABC;
(Ⅱ)求四棱锥A-BCDE的体积.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)首先,证明DE⊥AC,然后结合DE∥BC,得到BC⊥平面ADC,从而命题得证;
(2)可以过点A作AM⊥CD,得到AM⊥平面CBED,然后,根据体积公式求解.
(2)可以过点A作AM⊥CD,得到AM⊥平面CBED,然后,根据体积公式求解.
解答:
 证明:(1)∵D、E是边AC、AB的中点,即DE是VABC的中位线,
证明:(1)∵D、E是边AC、AB的中点,即DE是VABC的中位线,
∴DE⊥AC,
∵DE⊥DC,
∴DE⊥平面ADC,
∵DE∥BC,
∴BC⊥平面ADC,
∴面ADC⊥面ABC;
(2)过点A作AM⊥CD,
∴AM⊥平面CBED,
∵M是DC的中点,AM=
,
∴四棱锥A-BCDE的体积V=
×
×
×
.
=
.
 证明:(1)∵D、E是边AC、AB的中点,即DE是VABC的中位线,
证明:(1)∵D、E是边AC、AB的中点,即DE是VABC的中位线,∴DE⊥AC,
∵DE⊥DC,
∴DE⊥平面ADC,
∵DE∥BC,
∴BC⊥平面ADC,
∴面ADC⊥面ABC;
(2)过点A作AM⊥CD,
∴AM⊥平面CBED,
∵M是DC的中点,AM=
| 3 |
| 4 |
∴四棱锥A-BCDE的体积V=
| 1 |
| 3 |
| 3 |
| 4 |
| ||
| 2 |
| ||
| 2 |
=
3
| ||
| 32 |
点评:本题综合考查了空间中垂直关系及其判断、体积公式的应用等知识,属于中档题.

练习册系列答案
相关题目
如图,正方体ABCD-A1B1C1D1中,直线AB1与BC1所成角为( )


| A、30° | B、45° |
| C、60° | D、90° |