题目内容
已知二次函数f(x)=x2+x,若不等式f(-x)+f(x)≤2|x|的解集为C.
(1)求集合C;
(2)若方程f(ax)-ax+1=5(a>0,a≠1)在C上有解,求实数a的取值范围.
(1)求集合C;
(2)若方程f(ax)-ax+1=5(a>0,a≠1)在C上有解,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由f(x)=x2+x,代入f(-x)+f(x)≤2|x|,去掉绝对值求解即可;
(2)利用换元法求解关于指数函数的方程.
(2)利用换元法求解关于指数函数的方程.
解答:
解:(1)f(x)+f(-x)=2x2------------------------------(1分)
当x≥0时,2x2≤2x
解得:0≤x≤1------------------(3分)
当x<0时,2x2≤-2x
解得:-1≤x<0--------------(5分)
所以集合C=[-1,1]---------------(6分)
(2)∵f(ax)-ax+1-5=0
∴(ax)2-(a-1)ax-5=0,
令ax=u
则方程为h(u)=u2-(a-1)u-5=0,
h(0)=-5---------------(7分)
当a>1时,u∈[
,a],h(u)=0在[
,a]上有解,
则
∴a≥5-----------------(9分)
当0<a<1时,u∈[a,
],g(u)=0在[a,
]上有解,
则
∴0<a≤
------------------------(11分)
所以,当0<a≤
或a≥5时,方程在C上有解,且有唯一解.-----------(12分)
当x≥0时,2x2≤2x
解得:0≤x≤1------------------(3分)
当x<0时,2x2≤-2x
解得:-1≤x<0--------------(5分)
所以集合C=[-1,1]---------------(6分)
(2)∵f(ax)-ax+1-5=0
∴(ax)2-(a-1)ax-5=0,
令ax=u
则方程为h(u)=u2-(a-1)u-5=0,
h(0)=-5---------------(7分)
当a>1时,u∈[
| 1 |
| a |
| 1 |
| a |
则
|
∴a≥5-----------------(9分)
当0<a<1时,u∈[a,
| 1 |
| a |
| 1 |
| a |
则
|
∴0<a≤
| 1 |
| 2 |
所以,当0<a≤
| 1 |
| 2 |
点评:本题主要考查二次函数的性质,有关指数的方程.

练习册系列答案
相关题目
已知集合M={x|log3x≤1},N={x|x2-2x<0},则( )
| A、M=N | B、M∩N=∅ |
| C、M∩N=R | D、N⊆M |
已知{an}是等差数列,a1+a7=-2,a3=2,则{an}的公差d=( )
| A、-1 | B、-2 | C、-3 | D、-4 |
正方体ABCD-A1B1C1D1中,E、F分别是AA1、AB的中点,则EF与对角面BDD1B1所成角的度数是( )
| A、30° | B、45° |
| C、60° | D、150° |
函数y=lg(-x2-3x+4)的定义域是( )
| A、(-4,-1) |
| B、(-4,1) |
| C、(-1,4) |
| D、[-4,1] |
已知向量
=(an,-1),
=(2,an+1),n∈N*且a1=2,
⊥
,则数列{an}的前n项和为Sn=( )
| a |
| b |
| a |
| b |
| A、2n+1-2 |
| B、2-2n+1 |
| C、2n+1 |
| D、3n-1 |
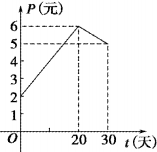 某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示:
某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示: