题目内容
已知集合M={x|log3x≤1}，N={x|x2-2x＜0}，则（ ）
| A、M=N | B、M∩N=∅ |
| C、M∩N=R | D、N⊆M |
考点：对数函数的单调性与特殊点,交集及其运算
专题：函数的性质及应用
分析：解对数不等式求得M，解一元二次不等式求得N，从而得到M、N间的关系．
解答：
解：∵集合M={x|log3x≤1}={x|0＜x≤3}，N={x|x2-2x＜0}={x|0＜x＜2}，
∴N⊆M，
故选：D．
∴N⊆M，
故选：D．
点评：本题主要考查对数不等式、一元二次不等式的解法，两个集合间的包含关系，属于基础题．
练习册系列答案
相关题目
函数f（x）=2x-x2在区间（0，3）上的最大值、最小值分别为（ ）
| A、1，-3 |
| B、0，-3 |
| C、无最大值，-3 |
| D、1，无最小值 |
椭圆2x2+3y2=6的焦距是（ ）
| A、2 | ||||
B、2（
| ||||
C、2
| ||||
D、2（
|
四面体ABCD的四个顶点都在球O的表面上，AB⊥平面BCD，△BCD是边长为3的等边三角形．若AB=2，则球O的表面积为（ ）
| A、4π | B、12π |
| C、16π | D、32π |
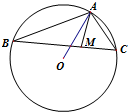如图所示，O为△ABC的外接圆圆心，AB=10，AC=4，∠BAC为钝角，M是边BC的点，且满足| BM |
| MC |
| AM |
| AO |
| A、21 | B、22 | C、29 | D、36 |