题目内容
正方体ABCD-A1B1C1D1中,E、F分别是AA1、AB的中点,则EF与对角面BDD1B1所成角的度数是( )
| A、30° | B、45° |
| C、60° | D、150° |
考点:直线与平面所成的角
专题:计算题,空间角
分析:由正方体的几何特征,及E、F分别是AA1、AB的中点,连接A1C1交B1D1于O,则∠A1BO即为EF与对角面BDD1B1所成角,解Rt△BA1O即可求出EF与对角面BDD1B1所成角的度数.
解答:
解:∵E、F分别是AA1、AB的中点,
∴EF∥A1B,
则EF与对角面BDD1B1所成角等于A1B对角面BDD1B1所成角
连接A1C1交B1D1于O
由正方体的几何特征可得A1C1⊥平面BDD1B1.即∠A1BO即为EF与对角面BDD1B1所成角
在Rt△BA1O中,∵BA1=2A1O
∴∠A1BO=30°
故选A
∴EF∥A1B,
则EF与对角面BDD1B1所成角等于A1B对角面BDD1B1所成角
连接A1C1交B1D1于O
由正方体的几何特征可得A1C1⊥平面BDD1B1.即∠A1BO即为EF与对角面BDD1B1所成角
在Rt△BA1O中,∵BA1=2A1O
∴∠A1BO=30°
故选A
点评:本题考查的知识点是直线与平面所成的角,其中根据正方体的几何特征,求出EF与对角面BDD1B1所成角对应的平面角,将空间线面夹角转换为解三角形问题是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=2x-x2在区间(0,3)上的最大值、最小值分别为( )
| A、1,-3 |
| B、0,-3 |
| C、无最大值,-3 |
| D、1,无最小值 |
四面体ABCD的四个顶点都在球O的表面上,AB⊥平面BCD,△BCD是边长为3的等边三角形.若AB=2,则球O的表面积为( )
| A、4π | B、12π |
| C、16π | D、32π |
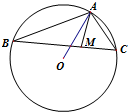 如图所示,O为△ABC的外接圆圆心,AB=10,AC=4,∠BAC为钝角,M是边BC的点,且满足
如图所示,O为△ABC的外接圆圆心,AB=10,AC=4,∠BAC为钝角,M是边BC的点,且满足| BM |
| MC |
| AM |
| AO |
| A、21 | B、22 | C、29 | D、36 |
两个半球为1的铁球,熔化后铸成一个球,这个大球的半径为( )
| A、2 | |||||
B、
| |||||
C、
| |||||
D、
|