题目内容
设函数f(x)=-x2+ax+3(a>0).
(1)求函数y=f(x)最大值;
(2)若函数在(0,3)上有零点,求实数a的取值范围;
(3)对于给定的正数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立,求l(a)表达式,并求函数l(a)最大值.
(1)求函数y=f(x)最大值;
(2)若函数在(0,3)上有零点,求实数a的取值范围;
(3)对于给定的正数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立,求l(a)表达式,并求函数l(a)最大值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)利用配方法求二次函数的最值;
(2)根据零点的判定方法,得f(0)=3>0,固有f(3)<0;
(3)分情况进行讨论.
(2)根据零点的判定方法,得f(0)=3>0,固有f(3)<0;
(3)分情况进行讨论.
解答:
解:(1)f(x)=-x2+ax+3=-(x-
)2+
a2+3,
故函数最大值fmax=
a2+3,
(2)由题意,因为f(0)=3>0,图象开口朝下,
则必有f(3)<0,
解得a∈(0,2);
(3)由f(x)=-x2+ax+3=-(x-
)2+
a2+3,
当
a2+3>5时,即a>2
,
l(a)是方程-x2+ax+3=5的较小根,
解得l(a)=
;
当
a2+3≤5时,即0≤a≤2
时,
l(a)是方程-x2+ax+3=-5的较大根,
解得l(a)=
;
综上:l(a)=
---------(7分)
(3)当0≤a≤2
时,l(a)=
≤
=
+
当a>2
时,l(a)=
=
<
=
对比可知:当a=2
时,l(a)取到最大值
+
---------(10分)
| a |
| 2 |
| 1 |
| 4 |
故函数最大值fmax=
| 1 |
| 4 |
(2)由题意,因为f(0)=3>0,图象开口朝下,
则必有f(3)<0,
解得a∈(0,2);
(3)由f(x)=-x2+ax+3=-(x-
| a |
| 2 |
| 1 |
| 4 |
当
| 1 |
| 4 |
| 2 |
l(a)是方程-x2+ax+3=5的较小根,
解得l(a)=
a-
| ||
| 2 |
当
| 1 |
| 4 |
| 2 |
l(a)是方程-x2+ax+3=-5的较大根,
解得l(a)=
a+
| ||
| 2 |
综上:l(a)=
|
(3)当0≤a≤2
| 2 |
a+
| ||
| 2 |
2
| ||||
| 2 |
| 2 |
| 10 |
当a>2
| 2 |
a-
| ||
| 2 |
| 4 | ||
a+
|
| 4 | ||||
2
|
| 2 |
对比可知:当a=2
| 2 |
| 2 |
| 10 |
点评:本题主要考查二次函数的单调性、最值、零点等知识,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
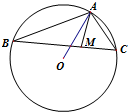 如图所示,O为△ABC的外接圆圆心,AB=10,AC=4,∠BAC为钝角,M是边BC的点,且满足
如图所示,O为△ABC的外接圆圆心,AB=10,AC=4,∠BAC为钝角,M是边BC的点,且满足| BM |
| MC |
| AM |
| AO |
| A、21 | B、22 | C、29 | D、36 |
在△ABC中,已知2
asinB=3b且cosB=cosC,A为锐角,则△ABC的形状为( )
| 3 |
| A、等边三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
已知命题p:2≤2;q:
是有理数,则下列命题为真命题的是( )
| 2 |
| A、p∧q | B、p∧¬q |
| C、¬p∧q | D、¬p∧¬q |