题目内容

函数y=lg（-x2-3x+4）的定义域是（　　）
A、（-4，-1）
B、（-4，1）
C、（-1，4）
D、[-4，1]
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：直接由对数式的真数大于0，求解一元二次不等式得答案．
解答： 解：由-x2-3x+4＞0，得x2+3x-4＜0，即（x+4）（x-1）＜0，解得-4＜x＜1．
∴函数f（x）=lg（-x2-3x+4）的定义域为（-4，1）．
故选：B．
点评：本题考查了函数的定义域及其求法，考查了一元二次不等式的解法，是基础题．
练习册系列答案
相关题目
已知数列{an}是等差数列，且a1=2，a1+a2+a5=12．
（1）求数列{an}的通项公式；
（2）令bn=an+2n，求数列{bn}的前n项和Sn．
椭圆2x2+3y2=6的焦距是（　　）
A、2
B、2（
3
-
2
）
C、2
5
D、2（
3
+
2
）
已知二次函数f（x）=x2+x，若不等式f（-x）+f（x）≤2|x|的解集为C．
（1）求集合C；
（2）若方程f（ax）-ax+1=5（a＞0，a≠1）在C上有解，求实数a的取值范围．
已知双曲线mx2-ny2=1（mn＞0）的渐近线方程为y=±
3
4
x，此双曲线的离心率为（　　）
A、
5
3
B、
5
4
C、
5
4
或
5
3
D、
7
4
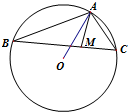如图所示，O为△ABC的外接圆圆心，AB=10，AC=4，∠BAC为钝角，M是边BC的点，且满足
BM
=2
MC
，则
AM
•
AO
=（　　）
A、21B、22C、29D、36
某市为了倡导居民节约水资源，自来水实行分段收费．收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元，已知甲、乙两用户某月用水量为5：3．
（1）设甲用户用水量为5x，求该月甲、乙两户共交水费y元关于x的函数；
（2）若甲、乙两户该月共交水费26.4元，求出甲、乙两户该月的用水量和水费．
在△ABC中，已知2
3
asinB=3b且cosB=cosC，A为锐角，则△ABC的形状为（　　）
A、等边三角形
B、钝角三角形
C、直角三角形
D、等腰直角三角形
盒中有10只螺丝钉，其中有3只是坏的，现从盒中随机地抽取4个，那么概率是
3
10
的事件为（　　）
A、恰有1只是坏的
B、4只全是好的
C、恰有2只是好的
D、至多有2只是坏的

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网