题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,若ccosA+acosC=2bcosA.
(Ⅰ)求角A;
(Ⅱ)若△ABC的面积S=5
,b=5,求sinB.
(Ⅰ)求角A;
(Ⅱ)若△ABC的面积S=5
| 3 |
考点:正弦定理
专题:解三角形
分析:(I)由ccosA+acosC=2bcosA,利用正弦定理可得sinCcosA+sinAcosC=2sinBcosA,即sin(A+C)=2sinBcosA,再利用三角形内角和定理与诱导公式即可得出;
(II)由于△ABC的面积S=5
,b=5,可得5
=
bcsinA=
×5csin
,解得c.由余弦定理可得:a2=b2+c2-2bccosA,解得a.再利用正弦定理可得:
=
,解出即可.
(II)由于△ABC的面积S=5
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| a |
| sinA |
| b |
| sinB |
解答:
解:(I)∵ccosA+acosC=2bcosA,
∴由正弦定理可得sinCcosA+sinAcosC=2sinBcosA,
∴sin(A+C)=2sinBcosA,
∴sinB=2sinBcosA,
∵sinB≠0,
∴cosA=
,
∵A∈(0,π),
∴A=
.
(II)∵△ABC的面积S=5
,b=5,
∴5
=
bcsinA=
×5csin
,解得c=4.
由余弦定理可得:a2=b2+c2-2bccosA=52+42-2×5×4×cos
=21,
∴a=
.
由正弦定理可得:
=
,
∴sinB=
=
=
.
∴由正弦定理可得sinCcosA+sinAcosC=2sinBcosA,
∴sin(A+C)=2sinBcosA,
∴sinB=2sinBcosA,
∵sinB≠0,
∴cosA=
| 1 |
| 2 |
∵A∈(0,π),
∴A=
| π |
| 3 |
(II)∵△ABC的面积S=5
| 3 |
∴5
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
由余弦定理可得:a2=b2+c2-2bccosA=52+42-2×5×4×cos
| π |
| 3 |
∴a=
| 21 |
由正弦定理可得:
| a |
| sinA |
| b |
| sinB |
∴sinB=
| bsinA |
| a |
5sin
| ||
|
5
| ||
| 14 |
点评:本题考查了正弦定理、余弦定理、三角形内角和定理与诱导公式、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
经过空间任意三点作平面( )
| A、只有一个 |
| B、可作二个 |
| C、可作无数多个 |
| D、只有一个或有无数多个 |
已知α是平面,m,n是直线,则下列命题正确的是( )
| A、若m∥n,m∥α,则n∥α |
| B、若m⊥α,n∥α,则m⊥n |
| C、若m⊥α,m⊥n,则n⊥α |
| D、若m∥α,n∥α,则m∥n |
在△ABC中,角A、B、C的对边分别为a、b、c,若A=60°,a=
,b=2,则边长c等于( )
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
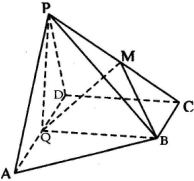 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=