题目内容
已知Sn为数列{an}的前n项和,且Sn=2an-2(n∈N*).
(1)求数列{an}的通项公式;
(2)在△ABC中,角A,B,C所对的边分别是3,a1,a2,求△ABC的面积.
(1)求数列{an}的通项公式;
(2)在△ABC中,角A,B,C所对的边分别是3,a1,a2,求△ABC的面积.
考点:数列递推式,三角形的面积公式
专题:等差数列与等比数列
分析:(1)由已知得an=2an-2an-1,n≥2,a1=2,由此能求出an=2n.
(2)由已知得△ABC的三边长为a=3,b=2,c=4,由此能求出△ABC的面积.
(2)由已知得△ABC的三边长为a=3,b=2,c=4,由此能求出△ABC的面积.
解答:
解:(1)∵Sn=2an-2(n∈N*),①
∴Sn-1=2an-1-2,n≥2,②
①-②,得an=2an-2an-1,n≥2
∴an=2an-1,n≥2
又S1=a1=2a1-2,解得a1=2,
∴an=2n.
(2)∵在△ABC中,角A,B,C所对的边分别是3,a1,a2,
∴△ABC的三边长为a=3,b=2,c=4,
∴cosB=
=
,
∴sinB=
=
,
∴S△ABC=
×3×4×
=
.
∴Sn-1=2an-1-2,n≥2,②
①-②,得an=2an-2an-1,n≥2
∴an=2an-1,n≥2
又S1=a1=2a1-2,解得a1=2,
∴an=2n.
(2)∵在△ABC中,角A,B,C所对的边分别是3,a1,a2,
∴△ABC的三边长为a=3,b=2,c=4,
∴cosB=
| 9+16-4 |
| 2×3×4 |
| 7 |
| 8 |
∴sinB=
1-
|
| ||
| 8 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 8 |
3
| ||
| 4 |
点评:本题考查数列的通项公式的求法,考查三角形的面积的求法,是中档题,解题时要注意三角形余弦定理的合理运用.

练习册系列答案
相关题目
“嫦娥一号”卫星的运行轨道是以地球的中心F为左焦点的椭圆,测得近地点A距离地面m千米,远地点B距地面n千米,地球的半径为k千米,关于椭圆以下3种说法正确的是( )
①焦距为(n-m)千米;②短轴长为2
千米;③离心率e=
.
①焦距为(n-m)千米;②短轴长为2
| (m+k)(n+k) |
| n-m |
| m+n+2k |
| A、① | B、①② | C、③ | D、①②③ |
如图所示,程序框图(算法流程图)的输出结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
命题p:双曲线2y2-x2=8的实轴长是2.命题q:抛物线y2=ax(a≠0)的准线是x=-
( )
| a |
| 4 |
| A、p或q是假命题 |
| B、¬p且q是真命题 |
| C、p且q是真命题 |
| D、p或¬q是真命题 |
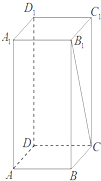 如图,正四棱柱ABCD-A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成角的大小为arctan
如图,正四棱柱ABCD-A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成角的大小为arctan