题目内容
已知函数f(x)=ax-bx(a>0,a≠1).
(1)若函数y=f(x)在(1,f(1))处的切线方程为y=(e-1)x,求函数f(x)的解析式;
(2)在(1)的条件下,设g(x)=x2-x+m,若存在x0∈R,使对任意x∈R不等式f(x)>g(x0)成立,求实数m的取值范围.
(1)若函数y=f(x)在(1,f(1))处的切线方程为y=(e-1)x,求函数f(x)的解析式;
(2)在(1)的条件下,设g(x)=x2-x+m,若存在x0∈R,使对任意x∈R不等式f(x)>g(x0)成立,求实数m的取值范围.
考点:利用导数研究曲线上某点切线方程,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)求出原函数的导函数,得到函数在x=1时的导数,然后结合题意求得a,b的值,则函数解析式可求;
(2)把存在x0∈R,使对任意x∈R不等式f(x)>g(x0)成立,转化为对任意x∈R,f(x)min>g(x)min成立,由二次函数求得g(x)的最小值,利用导数求得f(x)的最小值,然后列不等式求得m的取值范围.
(2)把存在x0∈R,使对任意x∈R不等式f(x)>g(x0)成立,转化为对任意x∈R,f(x)min>g(x)min成立,由二次函数求得g(x)的最小值,利用导数求得f(x)的最小值,然后列不等式求得m的取值范围.
解答:
解:(1)∵f(x)=ax-bx,
∴f′(x)=axlna-b,f′(1)=alna-b,
由函数y=f(x)在(1,f(1))处的切线方程为y=(e-1)x,得
,解得
.
∴f(x)=ex-x;
(2)f(x)=ex-x,g(x)=x2-x+m,
若存在x0∈R,使对任意x∈R不等式f(x)>g(x0)成立,即
对任意x∈R,f(x)min>g(x)min成立,
g(x)min=
,
f′(x)=ex-1,当x<0时,f′(x)<0,f(x)为减函数,当x>0时,f′(x)>0,f(x)为增函数,
∴函数f(x)的极小值也是最小值为f(0)=1.
由
<1,解得:m<
.
∴实数m的取值范围是(-∞,
).
∴f′(x)=axlna-b,f′(1)=alna-b,
由函数y=f(x)在(1,f(1))处的切线方程为y=(e-1)x,得
|
|
∴f(x)=ex-x;
(2)f(x)=ex-x,g(x)=x2-x+m,
若存在x0∈R,使对任意x∈R不等式f(x)>g(x0)成立,即
对任意x∈R,f(x)min>g(x)min成立,
g(x)min=
| 4m-1 |
| 4 |
f′(x)=ex-1,当x<0时,f′(x)<0,f(x)为减函数,当x>0时,f′(x)>0,f(x)为增函数,
∴函数f(x)的极小值也是最小值为f(0)=1.
由
| 4m-1 |
| 4 |
| 5 |
| 4 |
∴实数m的取值范围是(-∞,
| 5 |
| 4 |
点评:本题考查了利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,考查了利用导数求函数的最值,体现了数学转化思想方法,是中档题.

练习册系列答案
相关题目
已知函数f(x)=
,设方程f(x)=2-x+b(b∈R)的四个实根从小到大依次为x1,x2,x3,x4,对于满足条件的任意一组实根,下列判断中一定正确的为( )
|
| A、x1+x2=2 |
| B、1<x1x2<9 |
| C、0<(6-x3)(6-x4)<1 |
| D、9<x3x4<25 |
设a2-b2=c2、a=2b为空间两条不同的直线,α、β为两个不同的平面.下列命题中正确的是( )
| A、若a、b与α所成的角相等,则a∥b |
| B、若α⊥β,m∥α,则m⊥β |
| C、若a∥α,b∥β,α∥β,则a∥b |
| D、若b⊥α,b∥β,则α⊥β |
“嫦娥一号”卫星的运行轨道是以地球的中心F为左焦点的椭圆,测得近地点A距离地面m千米,远地点B距地面n千米,地球的半径为k千米,关于椭圆以下3种说法正确的是( )
①焦距为(n-m)千米;②短轴长为2
千米;③离心率e=
.
①焦距为(n-m)千米;②短轴长为2
| (m+k)(n+k) |
| n-m |
| m+n+2k |
| A、① | B、①② | C、③ | D、①②③ |
如图所示,程序框图(算法流程图)的输出结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
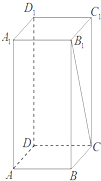 如图,正四棱柱ABCD-A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成角的大小为arctan
如图,正四棱柱ABCD-A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成角的大小为arctan