题目内容
共点力F1=（lg2，lg2），F2=（lg5，lg2）作用在物体M上，产生位移s=（2lg5，1），则共点力对物体做的功W为（ ）
| A、lg2 | B、lg5 | C、1 | D、2 |
考点：平面向量数量积的含义与物理意义
专题：计算题,平面向量及应用
分析：求出共点力的合力F=F1+F2，再求合力F对物体做的功W．
解答：
解：根据题意，得；
共点力的合力是
F=F1+F2=（lg2+lg5，lg2+lg2）=（1，2lg2）；
对物体做的功为
W=Fs=1×2lg5+2lg2×1=2（lg5+lg2）=2．
故选：D．
共点力的合力是
F=F1+F2=（lg2+lg5，lg2+lg2）=（1，2lg2）；
对物体做的功为
W=Fs=1×2lg5+2lg2×1=2（lg5+lg2）=2．
故选：D．
点评：本题考查了平面向量的应用问题，解题时应根据平面向量的数量积的意义进行解答，是基础题．
练习册系列答案
相关题目
如图，球O内切于圆柱O1O2．记球O的体积为V1，圆柱O1O2的体积为V2，则如图所示，程序框图（算法流程图）的输出结果是（ ）
| A、-3 | ||
B、-
| ||
C、
| ||
| D、2 |
已知双曲线方程为
-
=1，则双曲线的渐近线方程为（ ）
| x2 |
| 9 |
| y2 |
| 3 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±3x |
若实数a、b满足a+b=1，则3a+3b的最小值是（ ）
| A、18 | |||
B、2
| |||
| C、6 | |||
D、2
|
执行如图所示的程序框图，则输出的结果可以是（ ）
| A、2lnx |
| B、cosx |
| C、x-2 |
| D、e|x| |
已知A、B、D三点共线，则对任意一点C，有
=
+λ
，则λ=（ ）
| CD |
| 4 |
| 3 |
| CA |
| CB |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设m、n为两条不同直线，α、β为两个不同平面，则下列命题正确的是（ ）
| A、若m∥α，n∥β，m∥n，则α∥β |
| B、若m⊥α，n⊥β，m⊥n，则α⊥β |
| C、若α∥β，m?α，n?β，则m∥n |
| D、若α⊥β，α∩β=m，n⊥m，则n⊥β |
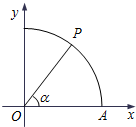如图，曲线Γ：x2+y2=1（x≥0，y≥0）与x轴交于点A，点P在曲线Γ上，∠AOP=α．