题目内容
设m、n为两条不同直线,α、β为两个不同平面,则下列命题正确的是( )
| A、若m∥α,n∥β,m∥n,则α∥β |
| B、若m⊥α,n⊥β,m⊥n,则α⊥β |
| C、若α∥β,m?α,n?β,则m∥n |
| D、若α⊥β,α∩β=m,n⊥m,则n⊥β |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:根据线面、面面间的位置关系易知B正确.
解答:
解:若m∥α,n∥β,m∥n,则α∥β或α与β相交,故A错误;
若m⊥α,n⊥β,m⊥n,
则由平面与平面垂直的判定定理知α⊥β,故B正确;
若α∥β,m?α,n?β,则m与n平行或异面,故C错误;
若α⊥β,α∩β=m,n⊥m,
则n与β相交或n?β,故D不正确.
故选:B
若m⊥α,n⊥β,m⊥n,
则由平面与平面垂直的判定定理知α⊥β,故B正确;
若α∥β,m?α,n?β,则m与n平行或异面,故C错误;
若α⊥β,α∩β=m,n⊥m,
则n与β相交或n?β,故D不正确.
故选:B
点评:本题考查命题的真假判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
从1,2,3,4,5这5个数字中,任意抽取3个不同的数,这3个数的和为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
共点力F1=(lg2,lg2),F2=(lg5,lg2)作用在物体M上,产生位移s=(2lg5,1),则共点力对物体做的功W为( )
| A、lg2 | B、lg5 | C、1 | D、2 |
观察数列;-4,0,4,1,-4,0,4,1,-4,0,4,1…,则a2014=( )
| A、-4 | B、0 | C、4 | D、1 |
在复平面内,复数z=
的共轭复数对应的点位于( )
| 2i-1 |
| i-1 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
对于等式:cos4x=cos3x+cosx,下列说法正确的是( )
| A、对于任意x∈R,等式都成立 |
| B、对于任意x∈R,等式都不成立 |
| C、存在无穷多个x∈R使等式成立 |
| D、等式只对有限多个x∈R成立 |
已知集合A={x|x≤2},B={x|x(3-x)>0},则A∩B=( )
| A、{x|0<x≤2} |
| B、{x|x<0} |
| C、{x|x≤2,或x>3} |
| D、{x|x<0,或x≥2} |
已知数列数列{an}是等差数列,a3+a5+a7=21,求a5=( )
| A、5 | B、6 | C、7 | D、8 |
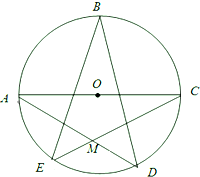 如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径.
如图,已知A,B,C,D,E均在⊙O上,且AC为⊙O的直径.