题目内容
若实数a、b满足a+b=1，则3a+3b的最小值是（ ）
| A、18 | |||
B、2
| |||
| C、6 | |||
D、2
|
考点：基本不等式
专题：不等式的解法及应用
分析：由基本不等式可得3a+3b≥2
=2
=2
，注意等号成立的条件即可．
| 3a•3b |
| 3a+b |
| 3 |
解答：
解：∵3a＞0，3b＞0，a+b=1，
∴3a+3b≥2
=2
=2
当且仅当a=b=
时取等号，
∴3a+3b的最小值是2
故选：D
∴3a+3b≥2
| 3a•3b |
=2
| 3a+b |
| 3 |
当且仅当a=b=
| 1 |
| 2 |
∴3a+3b的最小值是2
| 3 |
故选：D
点评：本题考查基本不等式，涉及指数的运算，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
设P是圆（x-3）2+（y+1）2=4上的动点，Q是直线x=-3上的定点（-3，-1），则|PQ|的最小值与最大值之和为（ ）
| A、10 | B、8 | C、12 | D、14 |
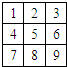用红、黄、蓝三种颜色去涂题图中标号为1，2，…，9的9个小正方形，使得任意相邻（有公共边）的小正方形所涂的颜色不同，且“3、5、7”号数字涂色相同，则符合条件的所有涂法种数为（ ）| A、96 | B、108 |
| C、196 | D、432 |
已知集合M={x|x＜3}，N={x|2＜x＜4}，则M∩N=（ ）
| A、∅ |
| B、{x|0＜x＜3} |
| C、{x|1＜x＜3} |
| D、{x|2＜x＜3} |
共点力F1=（lg2，lg2），F2=（lg5，lg2）作用在物体M上，产生位移s=（2lg5，1），则共点力对物体做的功W为（ ）
| A、lg2 | B、lg5 | C、1 | D、2 |
二项式（x+2）10展开式中，二项式系数最大的项是（ ）
| A、第5项 | B、第6项 |
| C、第7项 | D、第5、6项 |
在复平面内，复数z=
的共轭复数对应的点位于（ ）
| 2i-1 |
| i-1 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |