题目内容
3.已知△ABC的外心P满足$3\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC}$,则cosA=( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 由$3\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC}$,得$3\overrightarrow{AB}•\overrightarrow{AP}={\overrightarrow{AB}}^{2}+\overrightarrow{AB}•\overrightarrow{AC}$,$3\overrightarrow{AC}•\overrightarrow{AP}=\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AC}}^{2}$
即$\frac{1}{2}{c}^{2}=bc•cosA$,$\frac{1}{2}{b}^{2}=bc•cosA$⇒b=c⇒cosA=$\frac{1}{2}$.
解答 解:∵△ABC的外心P满足$3\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC}$,
∴$3\overrightarrow{AB}•\overrightarrow{AP}={\overrightarrow{AB}}^{2}+\overrightarrow{AB}•\overrightarrow{AC}$,$3\overrightarrow{AC}•\overrightarrow{AP}=\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AC}}^{2}$,
∵$\overrightarrow{AP}•\overrightarrow{AB}=\frac{1}{2}{c}^{2},\overrightarrow{AP}•\overrightarrow{AC}=\frac{1}{2}{b}^{2}$
∴$\frac{1}{2}{c}^{2}=bc•cosA$,$\frac{1}{2}{b}^{2}=bc•cosA$⇒b=c⇒cosA=$\frac{1}{2}$.
故选:A
点评 本题考查了三角形外心定义,向量的数量积运算,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | -1或$\sqrt{3}$ | B. | 1或3 | C. | -2或6 | D. | 0或4 |
| A. | 正方形是平行四边形 | B. | 平行四边形的对角线相等 | ||
| C. | 正方形的对角线相等 | D. | 以上均不正确 |
(1)根据以上数据完成以下2×2列联表:
| 喜爱运 动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?参考公式:K2=$\frac{n(ad-b{c)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
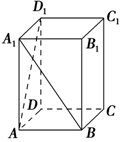 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.